The Foundations of Scientific Musical Tuning
by Jonathan Tennenbaum.
 |
Most figures and graphics are not included online.
Footnotes are at the
bottom of the page.
Other articles from this issue
This article is based on a speech given by the author, Director of the European Fusion Energy Foundation, at an April 1988 Schiller Institute conference on scientific tuning held in Milan, Italy. It appears also in the Institute's "Manual on the Rudiments of Tuning and Registration."
I want to demonstrate why, from a scientific standpoint, no musical tuning is acceptable which is not based on a pitch value for middle C of 256Hz (cycles per second), corresponding to A no higher than 432Hz. In view of present scientific knowledge, all other tunings including A=440 must be rejected as invalid and arbitrary.
Those in favor of constantly raising the pitch typically argue, "What difference does it make what basic pitch we choose, as long as the other notes are properly tuned relative to that pitch? After all, musical tones are just frequencies, they are all essentially alike. So, why choose one pitch rather than another?" To these people, musical tones are like paper money, whose value can be inflated or deflated at the whim of whoever happens to be in power.
This liberal philosophy of "free-floating pitch" owes its present power and influence in large part to the acoustical theories of Hermann Helmholtz, the nineteenth-century physicist and physiologist whose 1863 book, Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (The Theory of the Sensations of Tone as a Foundation of Music Theory) became the standard reference work on the scientific bases of music, and remains so up to this very day. Unfortunately, every essential assertion in Helmholtz's book has been proven to be false.
Helmholtz's basic fallacy—still taught in most music conservatories and universities today—was to claim that the scientific basis of music is to be found in the properties of vibrating, inert bodies, such as strings, tuning forks, pipes, and membranes. Helmholtz defined musical tones merely as periodic vibrations of the air. The fundamental musical tones, he claimed, are sine waves of various frequencies. Every other tone is merely a superposition of added-up sine waves, called "overtones" or "harmonics." The consonant musical intervals are determined by properties of the "overtone series" to be simple whole-number ratios of frequencies. Arguing from this standpoint, Helmholtz demanded that musicians give up well-tempering and return to a "natural tuning" of whole-number ratios; he even attacked the music of J.S. Bach and Beethoven for being "unnatural" on account of their frequent modulations.
Helmholtz based his theory of human hearing on the same fallacious assumptions. He claimed that the ear works as a passive resonator, analyzing each tone into its overtones by means of a system of tiny resonant bodies. Moreover, he insisted that the musical tonalities are all essentially identical, and that it makes no difference what fundamental pitch is chosen, except as an arbitrary convention or habit.
Helmholtz' theory: linear and wrong
Helmholtz's entire theory amounts to what we today call in physics a "scalar," "linear," or at best, "quasi-linear" theory. Thus, Helmholtz assumed that all physical magnitudes, including musical tones, can at least implicitly be measured and represented in the same way as lengths along a straight line. But, we know that every important aspect of music, of the human voice, the human mind, and our universe as a whole, is characteristically nonlinear. Every physical or aesthetic theory based on the assumption of only linear or scalar magnitudes, is bound to be false.
A simple illustration should help clarify this point. Compare the measurement of lengths on a straight line with that of arcs on the circumference of a circle. A straight line has no intrinsic measure; before we can measure length, we must first choose some unit, some interval with which to compare any given segment. The choice of the unit of measurement, however, is purely arbitrary.
The circle, on the contrary, possesses by its very nature an intrinsic, absolute measure, namely one complete cycle of rotation. Each arc has an absolute value as an angle, and the regular self-divisions of the circle define certain specific angles and arcs in a lawful fashion (e.g., a right angle, or the 120° angle subtended by the side of an equilateral triangle inscribed in the circle).
Just as the process of rotation, which creates the circle, imposes an absolute metric upon the circle, so also the process of creation of our universe determines an absolute value for every existence in the universe, including musical tones. Helmholtz refused to recognize the fact that our universe possesses a special kind of curvature, such that all magnitudes have absolute, geometrically-determined values. This is why Helmholtz's theories are systematically wrong, not merely wrong by accident or through isolated errors. Straight-line measures are intrinsically fallacious in our universe.
For example, sound is not a vibration of the air. A sound wave, we know today, is an electromagnetic process involving the rapid assembly and disassembly of geometrical configurations of molecules. In modern physics, this kind of self-organizing process is known as a "soliton." Although much more detailed experimental work needs to be done, we know in principle that different frequencies of coherent solitons correspond to distinct geometries on the microscopic or quantum level of organization of the process. This was already indicated by the work of Helmholtz's contemporary, Bernhard Riemann, who refuted most of the acoustic doctrines of Helmholtz in his 1859 paper on acoustical shock waves.1
Helmholtz's theory of hearing also turned out to be fallacious. The tiny resonators he postulated do not exist. The human ear is intrinsically nonlinear in its function, generating singularities at specific angles on the spiral chamber, corresponding to the perceived tone. This is an active process, akin to laser amplification, not just passive resonance. In fact, we know that the ear itself generates tones.
Moreover, as every competent musician knows, the simple sinusoidal signals produced by electronic circuits (such as the Hammond electronic organ) do not constitute musical tones. Prior to Helmholtz, it was generally understood that the human singing voice, and more specifically, the properly trained bel canto voice, is the standard of all musical tone. Historically, all musical instruments were designed and developed to imitate the human voice as closely as possible in its nonlinear characteristics.
The bel canto human voice is for sound what a laser is for light: The voice is an acoustical laser, generating the maximum density of electromagnetic singularities per unit action. It is this property which gives the bel canto voice its special penetrating characteristic, but also determines it as uniquely beautiful and uniquely musical. By contrast, electronic instruments typically produce Helmholtzian sine-wave tones, which are ugly, "dead," and unmusical exactly to the extent that they are incoherent and inefficient as electromagnetic processes.
Tuning is based on the voice
The human voice defines the basis for musical tuning and, indeed, for all music. This was clearly understood long before Helmholtz, by the scientific current associated with Plato and St. Augustine, and including Nicolaus of Cusa, Leonardo da Vinci and his teacher Luca Pacioli, and Johannes Kepler. In fact, Helmholtz's book was a direct attack on the method of Leonardo da Vinci.
|
If Helmholtz's theories are wrong, and those of Plato through Kepler and Riemann have been proven correct—at least as far as these went—then what conclusions follow for the determination of musical pitch today? Let us briefly outline the compelling reasons for C=256 Hz as the only acceptable scientific tuning, which have emerged from a review of the classical work of Kepler et al. as well as modern scientific research.
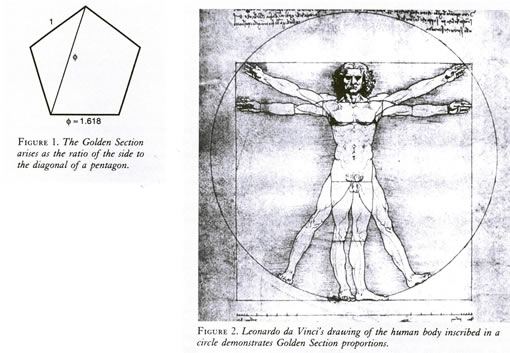
The human voice, the basic instrument in music, is also a living process. Leonardo and Luca Pacioli demonstrated that all living processes are characterized by a very specific internal geometry, whose most direct visible manifestation is the morphological proportion of the Golden Section. In elementary geometry, the Golden Section arises as the ratio between the side and the diagonal of a regular pentagon (see Figure 1). The Golden Section naturally forms what we call a self-similar geometric series—a growth process in which each stage forms a Golden Section ratio with the preceding one. Already before Leonardo da Vinci, Leonardo Pisano (also called Fibonacci) demonstrated that the growth of populations of living organisms always follows a series derived from the Golden Section. In extensive morphological studies, Leonardo da Vinci showed that the Golden Section is the essential characteristic of construction of all living forms. For example, Figure 2 illustrates the simplest Golden Section proportions of the human body.
Since music is the product of the human voice and human mind—i.e., of living processes—therefore, everything in music must be coherent with the Golden Section. This was emphatically the case for the development of Western music from the Italian Renaissance up through Bach, Mozart, and Beethoven.
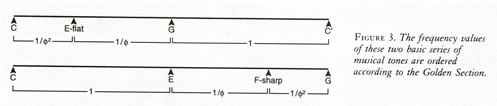
The Classical well-tempered system is itself based on the Golden Section. This is very clearly illustrated with the following two series of tones, whose musical significance should be evident to any musician: C—E- flat—G—C, and C—E—F-sharp—G. In the first series, the differences of the frequencies between the successive tones form a self-similar series in the proportion of the Golden Section. The frequency differences of the second series decrease according to the Golden Section ratio (see Figure 3).
The Golden Section
To understand the well-tempered system better, we must first examine the reason why certain specific proportions, especially the Golden Section, predominate in our universe, whereas others do not.
|
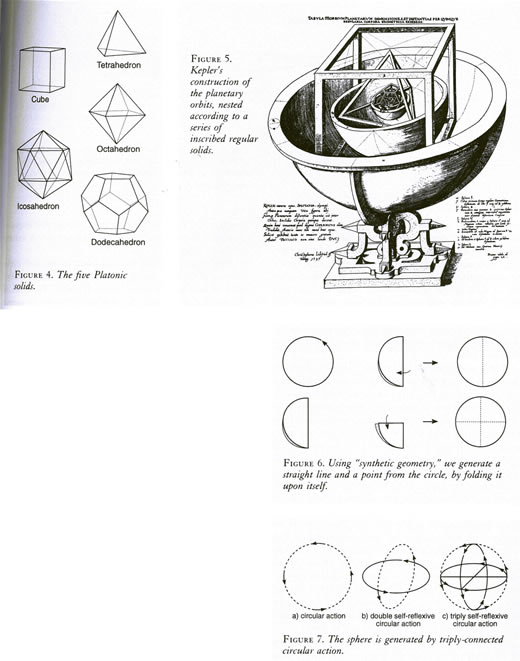
There is nothing mysterious or mystical about the appearance of the Golden Section as an "absolute value" for living processes. Space itself—that is, the visual space in which we perceive things—has a specific "shape" coherent with the Golden Section. For, space does not exist as an abstract entity independent of the physical universe, but is itself created. The geometry of space reflects the characteristic curvature underlying the process of generation of the universe as a whole. We know that space has a specific shape, because only five types of regular solids can be constructed in space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron (see Figure 4).
These five solids are uniquely determined characteristics of space. They are absolute values for all of physics, biology, and music. Indeed, Luca Pacioli emphasized that all the solids are derived from a single one, the dodecahedron, and that the latter is uniquely based upon the Golden Section. Hence, the Golden Section is the principal visual characteristic of the process of creation of the universe.
In his Mysterium Cosmographicum, Kepler provided further, decisive proof for Leonardo and Pacioli's method. He demonstrated that the morphology of the solar system, including the proportions of the planetary orbits, is derived from the five regular solids and the Golden Section. Figure 5 shows Kepler's famous construction of the planetary orbits through a nested series of concentric spheres, whose spacing is determined by inscribed regular solids. Therefore, the solar system has the same morphological characteristics as living organisms.
Kepler located the underlying reason for these morphological characteristics in the generating process of the universe itself, and this he attempted to identify with the help of what is called the isoperimetric theorem. This theorem states that among all closed curves having a given parameter, the circle is the unique curve which encloses the greatest area. Circular action is the maximally efficient form of action in visible space, and therefore coheres uniquely with the bel canto musical tone and the beam generated by a laser. Kepler reasoned that if circular action reflects uniquely the creative process of the universe, then the form of everything which exists—of atoms and molecules, of the solar system, and the musical system—must be constructible using nothing but circular action.
By this procedure, called "synthetic geometry," we generate from the circle, by folding it upon itself (i.e., circular action applied to itself), a straight line, the diameter. By folding again, we obtain a point, the center of the circle, as the intersection of two diameters, as in Figure 6. This alone creates for us the basic "elements" of plane geometry. Also, by rotating a circle we obtain the sphere (see Figure 7).
Further constructions, using circular action alone, generate the regular polygons—the equilateral triangle, square, and pentagon—which form the faces of the five regular solids. From these uniquely determined polygons, Kepler derived the fundamental musical intervals of the fifth, fourth, and major third, without any reference to overtones. These polygons embody the principle of self-division of circular action by 3, 4, and 5. The octave, or division by 2, we already obtained as the very first result of folding the circle against itself. From division by 2, 3, 4, and 5 we obtain, following Kepler, the following values for the basic musical intervals: octave, 1:2, fifth, 2:3, fourth, 3:4, major third, 4:5.
Division by seven is invalid, Kepler argued, because the heptagon is not constructible from circular action alone, nor does it occur in any regular solid. Since Kepler's musical ratios are uniquely coherent with the regular solids, they are uniquely coherent with the Golden Section underlying those solids.
Kepler went on to demonstrate that the angular velocities of the planets as they move in their elliptical orbits around the sun, are themselves proportioned according to the same ratios as the fundamental musical intervals (see Table I). Since Kepler's time, similar relations have been demonstrated in the system of moons of various planets, and provisionally also even in the motion of spiral galaxies.
|
C=256 as a "Keplerian interval"
C=256 has a uniquely defined astronomical value, as a Keplerian interval in the solar system. The period of one cycle of C=256 (
By contrast, A=440 is a purely arbitrary value, having no physical-geometrical justification. A=440 is an insane tuning in the rigorous sense that it bears no coherent relationship with the universe, with reality.
Today, we can add some essential points to this. Kepler's solution was absolutely rigorous, as far as it went; however, circular action is only an incomplete representation of creative action in the universe. The next great step was taken by Carl Friedrich Gauss at the beginning of the nineteenth century. Gauss introduced conical spiral action, instead of mere circular action, as the basis for synthetic geometry. Spiral action combines the isoperimetric principle of the circle with the principle of growth expressed by the Golden Section.
Let us demonstrate conical spiral action in the bel canto voice. Have a soprano sing a scale upward, starting at middle C (=256). As the frequency increases, so does the intensity of the sound produced. The more precise term for this intensity is "energy flux density." But this increase is not merely linear extension, not merely increase in scalar magnitude. As our singer sings upward, two important events occur. First, she must make a register shift, at F-sharp, in order to maintain the "isoperimetric," least-action form of bel canto tone. We shall return to the register shift in a moment. The second event occurs upon arrival at the octave, C=512. We hear very clearly, that one cycle of action has been completed, like a 360° rotation. This proves that there is a rotational component of action to increase the frequency or energy flux density. Again, Helmholtzian straight-line action does not exist.
|
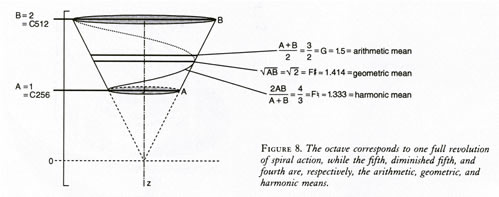
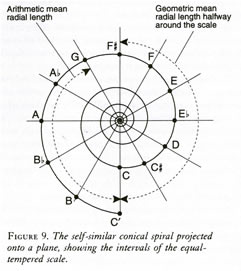
The true geometry of the singer's action is therefore most simply represented by spiral action upward on a cone. In Figure 8, the cone's axis represents frequency. Each circular cross-section of the cone represents a bel canto musical tone. The spiral makes one complete rotation in passing from C=256 to C=512, and one more cycle would bring it from C=512 to the next higher octave, C=1024. Thus, the interval of an octave corresponds to one complete 360° cycle of conical spiral action.
|
Not only the octave, but all musical intervals, correspond to specific angles on conical-spiral action. This is most clearly seen if we project our conical spiral onto a plane perpendicular to the axis (see Figure 9). If we divide a full 360° rotation into twelve equal angles, then each such (30°) displacement corresponds to a semitone interval in frequency. The radial lengths defined by the spiral at the indicated twelve angles are exactly proportional to the frequencies of the equal-tempered musical scale. The interval of a fifth corresponds to rotation through 7/12 of the circle, or 210°. The interval of a minor third corresponds to a right angle, and so forth.
(The equal-tempered system is only an approximation of a rigorous well-tempered system whose details have yet to be fully elaborated. Nevertheless, the indicated construction identifies the frequency regions and angular displacements within which the well-tempered values are to be defined.)
Most important, the halfway point of the full cycle starting at C, is F-sharp, the diminished fifth from C, or the interval once known as the "devil's interval." In terms of geometrical proportion, this F-sharp is located as the geometric mean of C=256 and its octave, C=512.
|
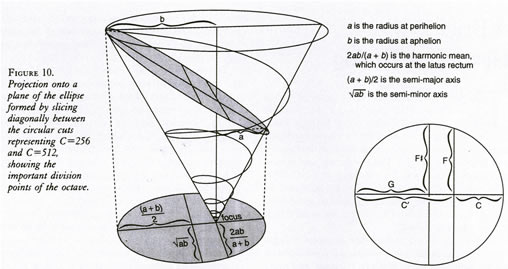
If we carry out synthetic geometry constructions with conical spiral action, just as Kepler did with circular action, we discover wonderful things. For example, construct the characteristic of the conical volume bounded by the circles at C=256 and C=512, by slicing the cone diagonally across those two circles. The result is an ellipse. Project this ellipse onto the plane. The principal parameters of the resulting plane ellipse define exactly the frequency ratios for the most important division-points of the octave (see Figure 10):
C=256 corresponds to the perihelion of the ellipse C=512 corresponds to the aphelion F corresponds to the semi-latus rectum F-sharp corresponds to the semi-minor axis G corresponds to the semi-major axis
At the same time, F, F-sharp, and G correspond to the harmonic, geometric, and arithmetic means, respectively, of the octave. These three means formed the basis of classical Greek theories of architecture, perspective, and music. The same notes F, F-sharp, and G mark the principal division of the basic C-major scale. This scale consists of two congruent tetrachords: C—D—E—F and G—A—B—C. The dividing-tone is F-sharp.
Physical significance of the register shift
Let us now return to our soprano. She makes the first register shift, from first to second register, exactly at this point of division. The first tetrachord, C—D—E—F, is sung in the first register, while G—A—B—C are sung in the second register. The register shift divides the scale exactly at the geometrical-mean or halfway point in the cycle of conical spiral action. The same process repeats in the next-higher octave, where the shift from second to third register of the soprano comes once again at F-sharp, the geometric mean.
The bel canto shift is a physical event of fundamental importance, and not merely a technical question for the voice. In physical terms, the register shift constitutes a singularity, a nonlinear phase change comparable to the transformation from ice to water or water to steam. An even better comparison is to the biological process of cell division (mitosis). In every case, we see that in C=256 tuning, the region of this singularity coincides with the principal geometrical division of conical spiral action. (Here we take the soprano voice, for musical and developmental reasons, as the fundamental reference for the human voice in general.)
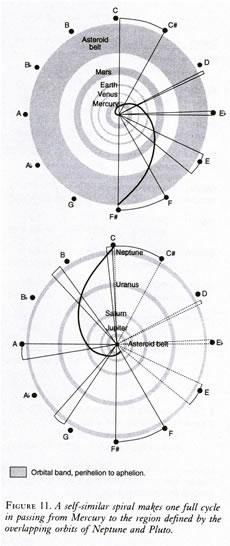
Our solar system also makes a "register shift." It has long been noted that the inner planets (Mercury, Venus, Earth, and Mars) all share such common features as relatively small size, solid silico-metallic surface, few moons, and no rings. The outer planets (Jupiter, Saturn, Uranus, and Neptune) share a second, contrasting set of characteristics: large size, gaseous composition, many moons, and rings. The dividing-point between these two sharply contrasting "registers" is the asteroid belt, a ring-like system of tens of thousands of fragmentary bodies believed to have arisen from an exploded planet.
|
It is easy to verify that the solar-system register shift falls exactly in the same, geometric-mean position, as the shift of the soprano voice in the proper C=256 tuning. If we begin at the outer layer of the sun, and construct a self-similar (logarithmic) spiral making exactly one rotation in passing from that layer to the orbit of the innermost planet, Mercury, then the continuation of that spiral will make exactly one full cycle in passing from Mercury to the region defined by the overlapping orbits of Neptune and Pluto (see Figure 11). The halfway or geometric-mean point comes exactly at the outer boundary of the asteroid belt. More precisely, if we compare the planetary spiral with our simple spiral derivation of the equal-tempered system, letting the interval from Mercury to Neptune-Pluto correspond to the octave C—C, then the planetary orbits correspond exactly in angular displacements to the principal steps of the scale. The asteroid belt occupies exactly the angular position corresponding to the interval between F and F-sharp; this region is where the soprano makes the register-shift, in C=256 tuning. Thus, complete coherence obtains, with this tuning, between the human voice, the solar system, the musical system, and the synthetic geometry of conical spiral action.2
|
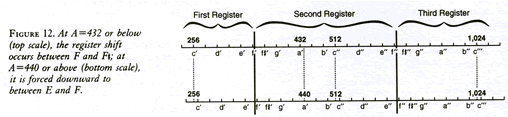
Figure 12 illustrates what happens if the tuning is arbitrarily raised, from C=256 (corresponding to A between 427Hz and 432Hz) to, for example, A=449. The soprano register shifts (at approximately 350Hz and 700Hz) lie, in the higher tuning, between E and F, rather than between F and F-sharp. This divides the octave in the wrong place, destroys the geometry of the musical system, destroys the agreement between music and the laws of the universe, and finally destroys the human voice itself.
If we arbitrarily changed the "tuning" of the solar system in a similar way, it would explode and disintegrate! God does not make mistakes: Our solar system functions very well with its proper tuning, which is uniquely coherent with C=256. This, therefore, is the only scientific tuning.
Notes
1. Bernhard Riemann, "Über die Fortpflanzung flacher Luftschwingungen von endlicher Weite," in Gesammelte mathematische Werke, ed. H. Weber (Leipzig, 1876), pp. 145-164. English translation: "On the Propagation of Plane Air Waves of Finite Amplitude," International Journal of Fusion Energy (1980), Vol. 2, No. 3.
2. Recent work by the late Dr. Robert Moon and associates has extended this coherence to the "microcosm" of subatomic physics.
Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews.