Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
 |
||
In reply to an inquiry concerning computer simulation of physical-economic process, Lyndon H. LaRouche, Jr., summarizes the role of creative cognition in education, in the arts and sciences, and in the history of man’s social development
For related articles, scroll down or click here.
Thank you for your communication. I summarize my knowledge of the crucial problems of computer simulation of physical- economic processes. I focus upon the presumption that such processes might be described mathematically as “meta-homeostatic” systems.
My discoveries in physical economy were developed in work conducted during the interval 1948-1952. This work was prompted by my adverse reaction both to certain included features of Prof. Norbert Wiener's text Cybernetics, and to related axiomatic fallacies central to Prof. John v. Neumann's notions of systems analysis. I recognized these fallacies of Wiener and v. Neumann, as a radically positivist expression of the same problem which I had addressed during my adolescence, in my defense of Leibniz's Monadology against those attacks on Leibniz which are the central feature of Immanuel Kant's celebrated three Critiques.
The outcome of that work may be summarized in three points. First, neither “information theory,” nor systems of simultaneous linear inequalities, may be employed to represent either the processes of human cognition, or mankind's historically-defined, efficient mastery of nature. Second, this implicitly poses the question; if the efficient impact of cognitive processes can not be pretermined in such ways, in what manner might the problem of measurement be addressed mathematically? Third, I recognized, that by relying upon the principle central to Bernhard Riemann's celebrated, 1854 habilitation dissertation, the problem of measurement could be solved: to conquer such problems, we must depart temporarily the domain of mathematical formalism, to continue our inquiry within the domain of experimental physics.1 Once we have discovered the relevant measurement of a successful demonstration of a physical principle, we return to mathematics, to rebuild mathematical physics in the revolutionary manner which the discovered principle requires.
During that 1948-1952 project, I employed the Leibniz approach to physical economy,2 as the domain in which to situate the problems of measurement. A 1952 rereading of Riemann's work from the vantage-point of my preceding discoveries in physical economy, guided me to my notions of an appropriate mathematical economics. Once some elementary conceptual problems were clarified, the practical approaches to mathematical representation become comprehensible.
The first task, is to isolate the determining function of the cognitive processes in shaping the performance of economy. This task is effectively situated, in first approximation, by demonstrating the paradoxical fallacy of the Malthusian assumption, that man were merely some species of higher ape. For that purpose, situate such an assumed, ape-like species, within the ecological conditions known to exist during the approximately two millions years of the present Ice Age.
That proposition yields estimated potential relative population-densities not exceeding several million individuals. (By “relative” population-density, one signifies that any otherwise determined cultural potential will vary as relative conditions of unimproved, improved, or depleted land-area, affect potential population-density.) The mathematician would consider any fixed range of values of potential relative population- densities, as corresponding, most conveniently, to a system defined by an axiomatically fixed theorem-lattice.
The evidence demonstrates that the human species is not of such an assumed, brutish type. The archeological and historical evidence is, that human potential relative population-density reached no higher than several hundred millions, throughout the planet, until Europe's Fifteenth Century, after which the impact of modern European civilization has prompted a rise of population to more than five billions individuals, with pre-1966 life- expectancies and conditions of life vastly superior to those existing in any part of the planet prior to the Fifteenth Century. Thus, we isolate the combination of both increases in potential relative population-density, and improvements in the demographic characteristics of populations; this serves us as the crucial variable for mathematical treatment.
The incorporation of wilful improvements in inhabitated land-areas, and in other technologies, should be considered by the mathematician, as in contrast to the fixed theorem-lattice of the “wild state” of mankind, the latter considered as if it were, ecologically, a “higher ape.” Thus, for purposes of mathematical description, the combined improvement in demographic characteristics and potential relative population-density, represent the equivalent of changes in the set of axioms and postulates underlying the brutish ecological potential. Thus, for purposes of formal estimations, the succession of significant increases of human population-potential defines a sequence of theorem-lattices, each transition in the form of the Riemann phase-shift mode, (n+1)/n. In every such transition, each lattice is separately formally from its predecessor by a formal, absolute discontinuity; this discontinuity corresponds to some axiomatic change in the hypothesis underlying the referenced theorem-lattice.3
Each such demographic level can be regarded as a special kind of disequilibriated state. That is, the increase of potential relative population-density in each such state, depletes the combination of previously existing and man-improved resources on which the characteristic technology of that state depends. This defines each theorem-lattice as a self-bounded system, which is disequilibriated by its convergence upon its bounds of that theorem-lattice mode expansion of population- density.
The introduction of a radical (axiomatic) change in technology, to a higher, similarly disequilibriated state, defines a new theorem-lattice, the latter of qualitatively increased growth of potential relative population-density, relative to the preceding theorem-lattice type.4
— Describing the Subject-Matter —
This picture prompts the introduction of a convenient, if somewhat crude classroom pedagogy. View such a succession of phase-shifts (theorem-lattices) in terms of relatively simple notions of “energy of the system” and “free energy.”
Indicate such notions of “energy of the system” and “free energy” to signify an array of measurements of the following type. Define both consumption and production in terms of four classes of “market-baskets” required to satisfy an indicated level of demographic (e.g., social-reproductive) potential: 1) Basic economic infrastructure, as a) physical improvements in land-area used, b) essential services such as education, heath, and science and technology development per se; 2) households' consumption of physical goods, plus education, health, and science-technology services; 3) Manufacturing and other industrial production; and 4) Necessary administration. Determine “free energy,” as the amount of total production of these contents of market-baskets which is in excess of “energy of the system” requirements for consumption by that society. Measure each of the elements of these four-plus classes of market-baskets of consumption and output, in terms of per-capita values (of imputable labor-force), per-household values, and per- square-kilometer values of implicitly used land-area.
Derive the notion of a ratio of “free energy” to “energy of the system” from the foregoing considerations. Specify, that the successful continuation (social reproduction = growth of potential relative population-density) of society, requires that this ratio of “free energy” to “energy of the system” not decrease, despite required increases in the absolute content of the market-baskets employed to define “energy of the system.”
In effect, this also signifies, that the conversion of “free energy” into productive capital, thus increasing the capital- intensity of the social-reproductive process (e.g., per capita and per square kilometer), must increase the per-capita rate of generation of “free energy” in those terms. This constraint identifies, in first approximation, the notion of the required “not-entropy” of the social-economic process as a whole.
— The Function of Cognition —
Since the efficient function of cognitive processes in science and in technological progress is rarely addressed in a rigorous way, I should identify for your convenience the relevant manner in which I define and approach this problem. My representation of a “not-entropic” function in social processes, is derived from this treatment of cognition.
Currently, to identify the function of cognition for my students and associates, I use a pair of examples from the history of science. These examples are correlated with what Riemann's habilitation dissertation implicitly defines as the mathematical type of a revolution in mathematical physics.
First, to illustrate the principled way in which a valid discovery of principle occurs, I prefer the case of Eratosthenes' estimate of the meridian; this example affords a desirable minimum of diverting mathematical considerations, thus focussing attention more immediately upon the fact that Eratosthenes estimated a curvature not to be seen by man until approximately twenty-two centuries later. I identify that as representing the type of idea of a measurable effect, an idea of a physical principle, for which no direct, single sensory object of reference exists for the discoverer's sense-perception at that time.
Such non-empiricist ideas are the elementary form of all valid scientific and classical-artistic work.
Second, I focus upon the combined, successive developments by Christiaan Huyghens, his student Ole Roemer, Leibniz, and Jean Bernouilli, in defining both the relativistic principle of isochronicity, and its application to identifying events occurring in a universe bounded internally by a fixed rate of retarded propagation of light. The required shift, from an algebraic to a “non-algebraic” (transcendental) mathematics, occasioned by this sequence of discoveries of principle, I identify as illustrating the type of Riemann phase-shift which experimental physics' discovery of a valid new principle, imposes as a revolution in mathematical physics. I identify that impact of experimental physics, in defining a higher ordering of a mathematical physics as typical of a “Riemann phase-shift,” the latter term referencing the kernel of Riemann's habilitation dissertation.
All valid discoveries of physical principles belong to the type of these kinds of non-empiricist ideas. Those principles, once validated in terms of an appropriate choice of crucial, measurable effect, function (as Riemann stated the relevant point) as new dimensions of a revised mathematical physics. This crucial measurement may occur either in the form of extension (e.g., a modified “Pythagorean yard-stick” = Gaussian “curvature”), or simply as the presence of a relevant discontinuity (singularity). Thus, experimental physics prompts us to overturn that naive, false notion of quadruply-extended, perfectly continuous space-time, which is sometimes identified as “Euclidean,” “Cartesian,” or “Newton-Maxwell” space-time.
Thus, each in a succession of new theorem-lattices appears, each among which which has no deductive consistency with its predecessor. That is the general, common aspect of a Riemann phase-shift relevant to the principal subject-matter of this communication. The relevant notion of cognition is located in the form of a question: What is the medium of action, external to any pre-existing, formal mathematical physics, by means of which the human mind causes experimental physics to generate a valid transition (Riemann phase-shift) from a theorem-lattice of “n,” to one of “n+1” dimensions? This action, as it occurs either in experimental physics, or classical art-forms, is the location of the event to be recognized as cognition.
As you will recognize, during the 18th and 19th Centuries, this issue became the central issue dividing modern mathematics and mathematical physics into two general camps, the camp of Kepler, Leibniz, Monge, Gauss, Riemann, et al., versus that of Fludd, Galileo, Descartes, Euler, Laplace, Helmholtz, et al., or, during the present century, such anti-Leibniz, anti-Riemann influentials as Bertrand Russell, “Bourbaki,” John v. Neumann, and Ilya Prigogine. The savage attack upon Max Planck by the followers of Ernst Mach, illustrates the point. My decades of experience with that controversy, prompts inclusion of the following qualifying interpolation here.
In a properly designed program of education, we educate the students, by leading them to re-experience, in their own mental processes, the act of original discovery of principle by the leading Classical Greeks, and by the successors to those Greek scientists and artists. The act of reexperiencing discoveries of principle, rather than memorizing them by repetition and reenforcement, is the practical definition of “knowledge,” as distinct from merely “learning.” One knows only if one has experienced the act of discovery of the valid principle in one's own mind: one knows only those valid ideas of principle which one has generated by means of one's own sovreign cognitive processes; knowledge is not fostered, but discouraged, by today's increasingly popular emphasis upon memorizing arbitrary dogma.
Knowledge acquired in that manner, has a double significance. Not only is it crucial and unique: the only means by which one may actually know a valid principle. It is familiarity with that quality of cognition, which is called up by reexperiencing, in proper succession, numerous, original valid discoveries of principle, beginning with those of the Classical Greeks, which fosters the emergence of the creative intellect in scientific and artistic work. It is the student's (for example) growing familiarity with that repeatedly reexperienced medium of creative discovery of valid principle, which enables the successful student to summon those cognitive processes to his aid, as when he is confronted by that type of paradox of principle which defies a well-established theorem-lattice in mathematical physics.
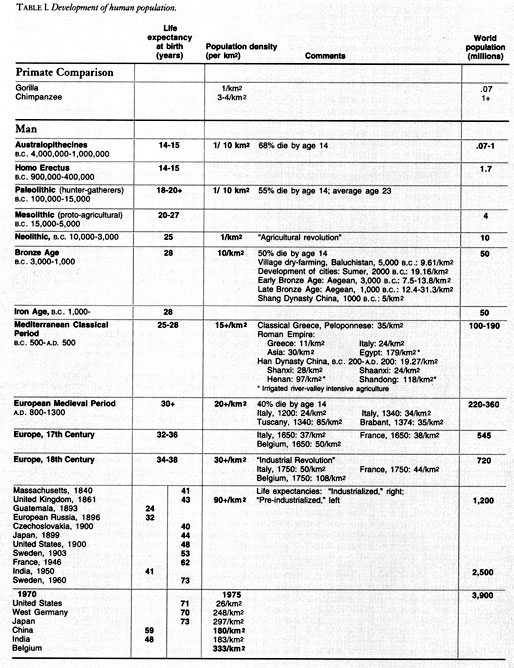
The increase of potential relative population-density (as illustrated by the enclosed figure and chart) is not entirely the result of discoveries of science; the progress of the Classical forms of art (as opposed to the so-called “Romantic” and “Modernist,” for example), is also premised upon discoveries of principle by the same faculty of creative cognition exhibited in discoveries of physical principle in science. Contrary to Kant and such neo-Kantians as the German proto-fascist Karl F. Savigny,5 there is, as the case of Leonardo da Vinci implies, a cognitive ordering principle in Classical forms of art which is identical in principle with that of fundamental progress in physical scientific knowledge.
Although no mathematical model of economic processes would attempt to program the artistic factor in social progress, the mathematician must take into account that potential margin of error in his “model” which might be introduced by excluding consideration of Classical art forms. For this reason, the mathematician must understand how this warning is to be applied, to understand what features of Classical-art principles must be borne in mind, if one is to avoid fallacy of composition in his construction of a mathematical image of economic progress.
— The Principle of Hypothesis —
In the most effective mode of education yet deployed, the European Classical Humanist model admired by Friedrich Schiller and his friend Wilhelm v. Humboldt, the development of the adolescent mind into the condition of an educated adult, began with the Homeric Greek epics, and continued through Classical Greek tragedy and the work of Plato and his Academy of Athens. This study provides the indispensable basis for coming to understand how scientific ideas are formed in the mind, and communicated. In this respect, the most important principles of natural science are presented most accessibly in the domain of Classical art-forms: epic and strophic poetry, Classical forms of tragedy (most emphatically, Aeschylos, Sophocles, Marlowe, Shakespeare, and Schiller), and the related notion of the Socratic dialogue, as employed by Plato.6 The following summary is included here, to demystify the principle of “hypothesis,” as that bears upon the mathematical problem which your message has placed under consideration in my response.
The central, explicit topic of the Homeric epics, the Iliad and the Odyssey, is man's relationship to the imagined gods of Olympus. The complementary, implicit topic, is the tragic character of that relationship, that the internal dynamic of the epics is leading to what the Greeks of Homer's time knew as the collapse of the Greek culture of the second millenium, B.C., into a prolonged, and devastating, “dark age.”7 These epics serve as the point of reference for the powerful form of tragedy associated with Aeschylos and Sophocles. The comparison of the Ulysses of the epic to the Prometheus of Aeschylos' Prometheus Bound, is exemplary.
In the Homeric epics, the emphasis is upon the distinctly different significance of the same event, in the experience of the gods of Olympus, and in the experience of mortal men and women. It is also the same in the Classical tragedy, as this is more faintly, but still definitely echoed in the tragedies of Marlowe and Shakespeare later.
Let us now consider the subjunctive mood, not as a grammatical form, but, rather, as a way of thinking. Treat the subjunctive, so conceived, as the natural setting for communication of the idea of hypothesis, as Plato and Riemann, for example, recognize hypothesis. After that is presented, turn next to the subject of metaphor, notably the fact that all ideas of physical principle come into existence in the individual human mind only in the form of metaphor. After that, consider the form which the mathematician must attribute to such metaphor and related ideas of physical principle. After that is done, we are prepared to focus upon the concluding point of this response to the communication received.
For this argument, think back to the Age of Pericles, and imagine an instance in which three Greeks share the experience of a certain distinct, troubling event in common. One of these Greeks is a person from Sparta, reared in the tradition of the Apollo cult's Lycurgus. Another is from Athens, reared in the memory of Solon. A third, viewed contemptuously by each of his two companions, is from Thebes. The two from Sparta and Thebes are each religious in their peculiarly pagan fashion; the perplexing event which they have just shared, prompts these two to see the hand of the pagan gods in both the experience and its import for the immediate future. There is much discussion, therefore, of the conduct of each of the sundry pagan gods of Olympos, during both Archaic and contemporary times.
The writer of such a bit of fiction, is thus obliged to situate the account of the relevant event, in terms of four, simultaneous, distinct, interacting theorem-lattices. Each of the three Greeks represents a distinct theorem-lattice; his idea of the event, and the practical action he is impelled to propose in response to it, is determined by the specific cultural matrix (theorem-lattice) of his city and social stratum. The gods of Olympus also represent a distinct cultural matrix, distinct from that of each of the three Greeks.
To wit: By theorem-lattice, we signify a (usually) open-ended collection of deductive, or analogous theorems, whose common feature is their lack of inconsistency with some, single, relatively fixed set of underlying axiomatic assumptions. The proposition which the mind of each will tend to form, in response to any perplexing (e.g., crucial) event, will be a proposition whose form is not inconsistent with such a relatively fixed set of axiomatic assumptions. In a word, each proposition will tend to be formed as not-inconsistent with an “hypothesis.”
In the interaction among the three Greeks, we are dealing with three mutually inconsistent cultural matrices, three mutually inconsistent theorem-lattices, three antagonistic hypotheses. How can one among these, the man from Athens, for example, conceptualize the propositions formulated in the opinion of his two companions? To state the critical point of this conjecture: How can the man from Athens form a series of judgments (propositions) identifying the propositions of each of his two companions? His proposition must qualify as a theorem of his cultural matrix, and yet must be a functional appreciation of the axiomatically inconsistent proposition formed in the mind of persons of axiomatically antagonistic cultural matrices. The state of mind imposed upon the man from Athens by this task, is exemplary of the subjunctive mood.
The subjunctive mood is the language of hypothesis.
Apply this view of the subjunctive mood to the three Greeks' discussion of the importance of the pagan gods in connection with the troubling event. The foremost problems are two: What do these gods believe (e.g., what is their propensity to act and react); how do the cultural matrices of these gods in contemporary times differ, if at all, from those of the gods of the Homeric epics? This takes the discussion among the three Greeks to a deeper level, to the level we recognize from Shakespeare as “a play within the play.”
This suggested piece of fiction poses an additional question. The conflict among cultural matrices —among hypotheses, so illustrated, implicitly poses a much deeper proposition. Since these sundry hypotheses differ axiomatically, which hypothesis is true? Is any among these hypotheses true? We have now re-situated our three Greeks as a play containing a play, all within a Socratic dialogue of Plato's type.
The most pervasive question which thus arises, in each and every consideration of that type, is: What is the relationship between relatively lesser or greater truthfulness, in the process of replacing one hypothesis by another. This is the problem posed, for example, by each crucial experimental test of a new physical principle. Plato would respond, that, given many hypotheses, ranked in order of the power over nature they afford, per capita, to society, that the succession of discoveries of principle consistent with such an ordering, corresponds to what Plato identifies as an “higher hypothesis,” a One subsuming a Many. He would respond, that the search for the truthfulness which the process of higher hypothesis seeks, is termed by him as “hypothesizing the higher hypothesis.”
Thus, the Many searchings for truth, if they are each relatively competent, each and all converge upon the single truthfulness of an adducible “hypothesizing of the higher hypothesis.” This would lead us directly to the issue of “metaphor,” but it were useful, perhaps indispensable, to take a very brief detour, to reconsider what we have just said about our fictional three Greeks.
The illustration we have just elaborated, has been chosen because it corresponds to the actual root of the development of the best feature of modern European civilization, a development which is implicitly traced to the emergence of the solar- astronomical calendars embedded within Vedic hymns of the Greeks' predecessors in Central Asia six thousand and more years ago. The ancient development of Classical epic and related poetry, and of the singing of that poetry, is the root of the finest products of the non-plastic arts, and also of scientific thinking. The development of Classical forms of geometry and poetry, are the roots and continuing foundations of civilized culture.
Until Europe's Fifteenth-Century formation of the modern form of nation-state, ninety-five percent or more of the people in every niche of humanity lived in a relative state of bestiality synonymous with slavery, serfdom, or worse. It was the affording of Classical education to orphans, and to other children, especially those from families of the poor, which produced an urban-centered stratum of educated recruits, chiefly from the ranks of the poor, the social formation upon which the replacement of feudalism by the modern nation-state was pioneered by France's King Louis XI, and others. It is the fostering of knowledge, through tendencies toward Classical forms of universal education, and the realization of that cultivated human potential, through fostering of investment in scientific and related progress in the productive powers of labor, which has made modern civilization possible. It is the role of the subjunctive, of the notion of hypothesis, and of metaphor, in early forms of composing and singing of epic and strophic poetry, through which the cultivation of the human mind for knowledge has progressed.
— Metaphor —
The idea of curvature in Eratosthenes' estimate for a Meridian, belongs to the type of discovery of a crucial principle of nature; it also illustrative of the type of Classical metaphor. By “metaphor,” one signifies a provable, efficient principle, which is first uttered without any symbolic or other correspondence to a literal sense-impression. It was approximately twenty-two centuries later, before any person saw the curvature of the Earth. Such an idea is an object of the process of cognition, not of perception. All scientific ideas are metaphors, and remain so in principle, even after we have assigned a literal name by which they might be recognized henceforth.8
The additional prerequisite of such a metaphor, is that it is efficient. That signifies that it is susceptible of demonstration, yielding some sense of measurement. The notion of “special relativity,” as defined in respect to both isochronism and a finite rate of retarded propagation of light, is such a metaphor. As I have noted above, the measurement may be in the form of a Pythagorean “yardstick” reflecting a demonstrable curvature of extension, or as a stubborn mathematical discontinuity, showing the presence of an efficient singularity. With those qualifications, any metaphor with the efficient character of a discovered, valid physical principle may be treated as a Riemann, geometry-analogous dimensionality in a phase-shift of the (n+1)/n type.
One of the most compelling examples of the way in which discoveries of physical principle increase the productive powers of labor, is provided by a Chase Econometrics report on the impact of the U.S.A.'s Kennedy Moon-landing project of the 1960s. The U.S. economy was given approximately fourteen dollars in increased income for each dollar spent on this aerospace research and development.
There are analogous effects in the domain of military spending. Although military consumption is economic waste, the role of technological attrition in modern warfare accelerates the advancement of the machine-tool and analogous sectors of the economy. We say that military consumption is generally waste, because it makes no contribution to social-reproductive processes within the cycle of production and consumption. However, the by- products of military procurement, such as increased and improved machine-tool capacity, do have reproductive significance for the productive sector of the economy. It is the transmission of new technologies to the non-military sector of the economy, through the impact of new technology on the tool-making sector, which has repeatedly caused U.S. high-technology military expenditures to increase the national income by a greater amount than was destroyed (economically) as military consumption per se.
There are similar effects registered in the role of development of “basic economic infrastructure,” in making possible increases in productive powers of labor, increases which could not have occurred without continued expansion and technological improvement of such elements of infrastructure as: transportation of increasing efficiency in ton-kilometers per hour, water management and general sanitation, production and distribution of power in increasing power-density (e.g., effective watts per square-centimeter cross-section), education, health care, and science and technology services.
The increase of the physical-productive powers of labor through advances in application of scientific and technological progress in a capital-intensive, power-intensive mode, is the immediate driver of increase in the potential relative population-density of society. This function depends upon a corresponding quality of relatively universal education, combined with a policy of fostering relatively high rates of investment in capital-intensive, power-intensive modes of technological progress in the society as a whole.
Thus, the determining role of “the subjective factor” of metaphor in fostering the increase of the productive powers of labor, and of potential relative population-density. This is measured, in effect, in terms of a constant or rising ratio of “not-entropy” (“free energy” to “energy of the system”) under conditions of increasing per-capita and per-square-kilometer ratios of capital- and power-intensity. This must take into account, losses occasioned by toleration of wasteful expenditures, including those of social parasitism; however, that noted, the principle should be clear.
The required mathematical model is obtained by recognizing the role of the isentropic-compression “shock” effect, in the internal functioning of a process which is governed by the combined principles of increasing capital-intensity, increasing power-intensity, and the imposed constraint of “not-entropy,” as I have identified that here. Under those conditions, a “meta- homeostatic” model would be a useful management tool.
— The Mathematical Problem Posed —
What are the mass and volume of the mental process —the thought— which generates, or regenerates, an original discovery of physical or analogous artistic principle? Such a mental process is of no appreciable magnitude: not zero, but incalculably (“transinfinitesimally”) nearly zero. In terms of conventional mathematics, such a thought is measured only as a transfinitely small mathematical discontinuity. Yet, this “magnitude” is efficient. It is the sole source of the “not- entropy” enabling that performance of economics which satisfies the “not-entropy” constraint indicated afresh in the immediately preceding paragraph.
To the best of my present knowledge the relevant functional connection between the generation, or regeneration of metaphor, on the one side, and the subjunctive expression of hypothesis, on the other side, was first made transparent in Plato's dialogues. I place special reference on the Phaedo, Meno, and Timaeus, treating each as addressing the solution to the ontological paradox posed by the Parmenides. I now summarize the implications of that for mathematical modelling of a modern economic process.
Given, an ordered sequence of valid hypotheses, each representing a greater potential power over nature, per capita, than its predecessor. Let such a sequence be addressed in the manner Plato, in the Parmenides confronts the Eleatics with the ontological paradox of the “One” and the “Many.” Treat the series of hypotheses as Plato treats a Many. What, under those constraints, is the One which efficiently subsumes the Many, defining the “Many” hypotheses, thus, as theorems of a theorem- lattice?
Examine the fashion in which this applies to either a Classical strophic form of poetry, or a song in the form of a Classical musical composition (as by Mozart, Beethoven, Schubert, or Brahms) employing a Classical strophic poem. Compare what we now report with the Ars Magna of the famous Raymond Llull.
The subject of such a Classical poem, or song, is the metaphor which defines the composition as a process brought to its close. (Any symbolic interpretation of such a poem is evidence of the student's incompetence in the matter.) This is a metaphor in the sense that Eratosthenes' estimate of the curvature of the Earth was a metaphor, or that the original form of the concept discovered to serve as a valid new physical principle, is a metaphor. How, then, shall this poem, or song, be performed?
Once the artist has recognized the metaphor which subsumes the poem or song as a whole process of development, he must now perform the poem or song under the governance of the certainty of the metaphor toward which the poem or song, appreciated as a developmental process, is leading. In a successful poem or song, this developmental process leads so with the force of that which Gottfried Leibniz defined as “necessary and sufficient reason.”
The relevant, crucial implications of that case, are the following. Once apprised by the performer, the concluding metaphor of a poem or song does not change at any time in the performer's conscious appreciation, as the performer is proceeding from the moment of silence which precedes the utterance into the momentary silence following the performance's close. Attempt to describe this mathematically, and the following paradox is presented. In the performance of that artistic composition, the performer's role is governed, in each moment of the proceeding, by a “memory of the future.” The “future” is represented by the controlling role of the concluding metaphor, throughout the performance. Thus, while, in each of its moments, the performance is developing from past through present, the course of that development is regulated by a principle which is acting efficiently from the relative future. It is the “collision” of efficient past with efficient future, in this way, which defines a singularity.
Such, in summary, is the relevant principle of “memory,” as this performs a central role in defining all Classical art forms, and in defining the meaning of the term “necessity” respecting notions of scientific principle. All processes are bounded by their outcome, in this specific sense. All valid abstract ideas, such as the idea of a crucial scientific principle, is defined in just this way.
Thus, the bounding of the economic process by the constraint of “not-entropy,” is to be read as a statement of the condition which a culture must satisfy, that it might survive. A culture which refuses to act according to that principle, will be destroyed by the nature whose condition it fails to satisfy. Once that point and its implications are apprehended, a competent mathematical approximation of the current phase of an economic process becomes a matter of the professional's knowledge, ingenuity, and persevering work.
Sincerely Yours,
Lyndon H. LaRouche, Jr.
|
Footnotes |
||
1. “Es fuehrt dies hinueber in das Gebiet einer andern Wissenschaft, in das Geibet der Physik, welches wohl die Natur der heutigen Veranlassung nicht zu betreten erlaubt.” Bernhard Riemann, “Ueber die Hypothesen, Welche der Geometrie zu Grunde liegen,” Bernhard Riemann's Gesammelte Mathematische Werke (New York: Dover Publications, 1956), p. 286.
2. “The Leibniz approach to physical economy” signifies, inclusively, the influence of Leibniz upon the patriotic American conspirators opposed to the immoral John Locke and the anti-scientific Adam Smith. This was the group gathered under the direction of Benjamin Franklin, including the authors of the U.S. Declaration of Independence, and the 1787-1789 design of the U.S.A. as a constitutional federal republic. What was known as the “American System of political-economy,” of U.S. Treasury Secretary Alexander Hamilton, the Careys, Henry Clay, John Quincy Adams, Friedrich List, and President Abraham Lincoln, is a direct product of Leibniz's influence. The same is to be said of the work of the French patriots Lazare Carnot and the Ecole Polytechnique under the direction of Gaspard Monge. Leibniz's communications to Czar Peter I are part of the corpus of Leibniz's work in founding the science of physical economy.
3. This signifies the use of “hypothesis,” in the Classical Greek sense, as by Leibniz and Riemann, not the illiterate's misuse of the term by Isaac Newton's admirers. That significance of “hypothesis,” is characteristic of Riemann's referenced habilitation dissertation; useful additional references are found on pages 524-538 of the referenced Werke. See also, the text of this present letter, below.
4. This imagery led to the later (1978) use of B. Riemann's 1860 model for isentropic compression [“Ueber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite”, op. cit., p. 156-175], as the model of reference for computer simulation of my economic forecasting “model” for the 1979-1983 U.S. economy.
5. The reference is to the hereditary influence of Kant's doctrine of aesthetics, as from Kant's Critique of Judgment, upon the neo-Kantian positivist Savigny. Savigny's famous ukase, decreeing an hermetic separation of Geisteswissenschaft (art, etc.) from Naturwissenschaft (natural science), is a point of emphasis here. In the final analysis, Kant's irrationalist doctrine of aesthetics is rightly seen as a continuation of the empiricist irrationalism of mathematician Thomas Hobbes' efforts to outlaw the subjunctive, hypothesis, and metaphor from modern language. Kant's difference with Hobbes and Locke on this point, is limited to Kant's abhorrence of the factor of “philosophical indifferentism” (intellectual crudity) in the work of his British empiricist teachers and other predecesors; it was Kant's more sophisticated defense of irrationalism, as defined in his attacks upon the crucial topics of Leibniz's Monadology, which provided the starting-point for the Nineteenth- Century continental aesthetics of such neo-Kantian irrationalists as J. G. Fichte, G. W. F. Hegel, Franz Liszt, Hector Berlioz, Richard Wagner, K. F. Savigny, and Friedrich Nietzsche.
6. This is a matter recently elaborated in considerable detail in instruction to staff and volunteers working in the writer's current campaign for the U.S. Democratic Party's 1996 presidential nomination. For example, the filming and editing of an extraordinarily successful, half-hour, nationwide television broadcast of March 2, 1996, on the NBC-TV network, was governed by the application of these principles.
7. The latter point, respecting the “new dark age,” has been emphasized by a collaborator.
8. In this sense, the term “metaphor” has the implication of Riemann's use of the alternate term Geistesmassen [Zur Psychologie und der Metaphysik, Werke, pp. 509- 520].
|
Figures and Tables |
||
What is the Schiller Institute?
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2004 All Rights Reserved.