|
|
|
The Geometry
|

Fidelio, Vol. IV,
No, 2. Summer 1995
For related articles, scroll down or click here.
The Metaphor of Perspective
by Pierre Beaudry
Introduction
The scientific idea of a nation-state, as opposed to the territorial looting of an empire, is based entirely on the willful purpose of fostering the common good of a population, and this commonwealth can only be achieved by means of improving the productive powers of labor of that population. In this fashion, the nation-state must be ruled in a dirigistic fashion, from a centralized government which commits itself to fostering man’s ability to reflect this general purpose through works in art and science. In turn, the elevated individual soul will ennoble the nation-state by bringing a contribution to its advancement and progress.
This is the general outlook which became predominant in France around the 1460’s, promoted chiefly through the influence of Nicolaus of Cusa and the school of the Brotherhood of the Common Life from Deventer. It was from this school that key collaborators of Leonardo da Vinci and France’s King Louis XI, such as Mathias Ringmann, Vautrin and Jean Lud, and Jean Pélerin Viator, came to establish themselves in Lorraine, the homeland of Joan of Arc and the crucial region in the creation of the nation-state of France which was then ruled by Duke René II.
From the standpoint of ennobling the individual, the nation-state should promote and defend the fundamental right of every human being to develop his mental powers of reason in imago Dei, and to perfect himself in order to get closer to the principle of composition of Divine Reason, the underlying principle of the Good that generates the changing relationships of all things in harmony with Natural Law.
In concrete terms, this means that the ruler of the nation-state must be committed to fostering man’s access to scientific knowledge, i.e., the discovery of the higher principles underlying the physical processes of nature, and the mastery of how to apply these to machine-tool principles and machines more generally. From this standpoint, the nation-state cannot exist without the explicit objective of establishing the principle of what Leibniz would later call “Academies” or “Societies”:
With the help of these Academies (or Societies), which are institutions of research and development, with their own manufactures and commercial houses directly attached to them, the monopolies will be eliminated, because the Academies will always guarantee a just and low price for the goods, and very often, such goods would become even cheaper because new manufactures will be built where none exist at that time.
Gottfried Wilhelm Leibniz,
“Society and Economy, Hanover, 1671”
These are the kinds of institutions that began to flourish in France under the leadership of King Louis XI, such as the Vosges Gymnasium, a Brotherhood of the Common Life school which had its own printing and distribution house. Later, this would be followed by the school of the Oratorians, the Royal Academy of Sciences, the Ecole Polytechnique of Gaspard Monge and Lazare Carnot, and the Ecole des Arts et Métiers [Arts and Trades]. Finally, this outlook would ulitmately be exported to Germany’s Göttingen University, and into the United States’ West Point Military Academy. In each and every case, the key to developing scientific method would be modeled on Nicolaus of Cusa’s teaching at the Council of Florence, and would be reflected in the rigorous approach of resolving paradoxes, expecially the paradox of the One and the Many, by means of constructive projective geometry.
This article will review the significance of projective geometry, or perspective, from the standpoint of a series of “nested” theorems developed over a period of three hundred years by lawful “predecessors” and “successors”—namely, Leonardo da Vinci-Jean Pélerin Viator (1505), Gérard Desargues (1639), Blaise Pascal (1645), Gaspard Monge (1794), and Jean-Victor Poncelet (1822). This long process of maturation involved a series of theorems, all of which contributed to developing a general synthetic approach to the understanding of the Euclidean plane, and laid the foundation for a science of constructive geometry as the definite and most lawful approach to the development of the creative process itself.
Indeed, there exists perhaps no single process of geometric discovery which has contributed more to increasing relative population-density in the world for the last five-hundred years, than the invention of perspective in France from the end of the Fourteenth to the end of the Eighteenth centuries. It would not be an exaggeration in the least to say that without this discovery initiated by the secretary of Louis XI, Jean Pélerin Viator, in collaboration with Leonardo da Vinci during the 1490 period, the industrial revolution made possible by Monge and Carnot some three hundred years later would not have been possible.
It would be on the basis of these discoveries made in the field of conical and orthographic projections that industrial designing would ultimately become the sine qua non condition for developing interchangeable parts in modern tool and machine-tool construction. In point of fact, there exist no household appliances in any home today that were not planned and designed, down to the last bolt, by such methods.
To begin, however, we must first present—by means of synthetic projective geometry—not a specialized form of geometry but a geometry of principles, what Lazare Carnot called a geometry of sentiment,1 which is aimed at moving the soul beyond the mediocrity of daily routines; a perspective aimed at directing man above the banalities of everyday life toward virtue, toward more noble sentiments, such as love of God, love of mankind, and love of country. In order to achieve this, you must acquire the sentiment of elevation, the sentiment of proportion, and the sentiment of the infinite. This is the crucial dividing line in the world today, as it has been throughout human history: whether human beings are treated as animals, or they are treated as created in the image of God.
For today, when the fate of mankind hangs in the balance, the same question that was posed two hundred years ago by the founders of the Ecole Polytechnique in the France of 1794, is again posed with renewed revolutionary vigor: will humanity be subjected to the barbarity of soul-less Aristotelian formalism, or will we succeed in reviving Platonic humanism, ruled by reason and guided by what the scientists of the French Renaissance tradition identified as le sentiment?
The Sentiment of Elevation
During the opening of his class on “Geometry and Mechanics Applied to the Arts” at the Conservatory of Paris in 1826, Jean-Victor Poncelet spoke the following amazing words, which show how the education of Polytechnique was oriented toward teaching the most advanced conception of science to ordinary workers:
Some people began to believe that mathematical truths were by necessity unintelligible to simple workers, because they are presented in abstract and difficult forms from dogmatic schoolbooks; some believed that they could not be easily understood and palpable: they were wrong. It was just that their method was at fault. There exists no mathematical principle, applicable to the works of the arts, that one cannot, with a little bit of study, manage to render easily intelligible to any individual with an ordinary intelligence. ...I would say to the pipefitter, the plumber, the boiler-maker, the lathe worker: When you make a diagonal cut across a pipe, a roll, or a funnel, you create an oval cut; and you, gardener, you trace the same oval with a rope and pickets. Now, suppose that your oval is more than two hundred million fathoms long; replace one of the pickets by an eternally gleaming ball, a sun which is 1,348,460 times larger than the Earth; and finally, make the Earth itself roll along an oval pathway at a speed of 23,000 fathoms per hour. Then you shall have an idea of the immense force with which the Almighty moves one of the smallest globes of one of the smallest worlds—worlds which include as many suns as you can imagine there are countable stars in the universe as a whole. Then, trace around that picket, the center of the sun, as many ovals as there are planets, and incline them more or less, and make them according to the length and width that I can give to you in numbers, and there you shall trace the pathways of the planets; and finally, each planet is the sun of its satellites and the focus of their ovals.
That is how we shall make easily understood to workers, the magnitude of our solar system and of the masses that compose it, with such a simple, beautiful, and should I say, divine ordering of the eternal movements that underlies these phenomena. This idea, which they will acquire in a few minutes, I say again, took centuries for disciplined people, respected for their works of art and science, to elevate themselves to the same level of knowledge.
—Jean-Victor Poncelet,
Opening statement to his class on
“Geometry and Mechanics Applied to the Arts,”
Conservatgory of Paris, 1826
- Master a discipline by means of internalizing its underlying principle.
- Apply the same underlying principle to another discipline.
- Embrace into one single theorem the unity of the underlying principle which bounds all disciplines of human industry.
From the standpoint of synthetic constructive geometry, what Poncelet identifies here is the process of creativity, the true sense of identity of the scientist, that is, of a true citizen of a sovereign nation-state; that is, not a specialist of some trade or art, but a universal man capable of understanding the necessity of developing the nation-state as a scientific idea. Indeed, this elevated sentiment implies for the student a mastery of the same underlying principle of change in both himself and in nature, in order for him to become the One, and his technological inventions for the nation, become the Many. In this way, Poncelet joins Lyndon LaRouche, isochronically, on the necessity of mastering the higher hypothesis2: this triply-self-reflexive principle illustrating the theorem of continuity whereby man is created in the image of God.
The Sentiment of Proportion
The most important thing to remember and to master properly is the sentiment of proportionality, that is, the theory of proportions or of the equality of relationships under consideration.
—Jean-Victor Poncelet,
Opening statement ot his class on “Industrial Mechanics,”
Metz, 1827
What kind of proportion exists between a bounding principle outside of the universe, and the harmonic ordering of the five Platonic solids inside of the universe? Kepler addressed this same question four-hundred years ago in attempting to understand the ratios between the celestial spheres. He wrote:
Wherefore it is clear that the very ratios of the planetary intervals from the sun have not been taken from the regular solids alone . . . . But it is consistent that if the Creator had any concern for the ratio of the spheres in general, He would also have had concern for the ratio which exists between the varying intervals of the single planets specifically, and that the concern is the same in both cases and the one is bound up with the other. If we ponder that, we will comprehend that for setting up the diameters and eccentricities conjointly, there is need fo more principles outside of the five regular solids.
—Johannes Kepler,
The harmony of the Spheres
* * *
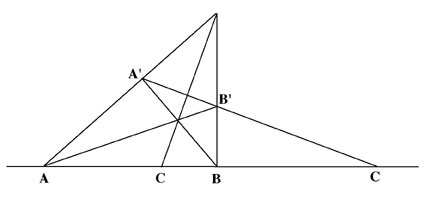
Given three arbitrary points A,B,C, on a straight line [See Figure 1], find with a ruler only, a fourth point D which shall be harmonically conjugated to the other three points in such a way that the four points compose a cross-ratio in the proportion3 DA : DB :: CA : CB.
FIGURE 1
Harmonic range ABCD, DA : DB :: CA : CB.
This projection is identified by Poncelet as a harmonic range, whose projective properties were well-known to the ancient Greeks, particularly Euclid. Charles Julien Brianchon, another student of the Ecole, had also arrived at the same results by establishing the following constant ratio:
AC : AD :: BC : BD = constant.
According to Poncelet, the Greeks had already defined this as the harmonic proportion in the following form:
(DA-DC) : (DC-DB) :: DA : DB.
A close examination of this last equality of relationship shows that this harmonic proportion uses only the distance of D to the other three points. This reflects the fact that the distance DC is known as the harmonic mean between the two distances DA and DB. Poncelet further noted that while the line AB is divided harmonically by points C and D, the reciprocal is also true, that is, CD is also divided harmonically by A and B.
Now, suppose that you position the three arbitrary points A,B,C in such a way that C is closer to A on the same straight line; then the fourth harmonic point D will be found on the opposite side of the same line [See Figure 2]. This amazing tilting of line A′B′ from right to left is the result of the reversing of the harmonic range, which can only occur when point D passes to infinity; and this is produced when infinite line DA is rotated into infinite line DB.
FIGURE 2
Harmonic range ABCD, DB : DA :: CB : CA
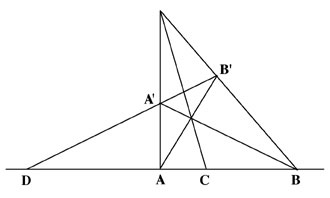
So, the reversing of the ratio is a very curious phenomenon indeed, which seems to be an exception to the rule of the theorem, and seems to cause an anomaly—because when the tilting from right to left occurs, the fourth harmonic point D is nowhere to be found on the straight line on which A,B, and C lie. Indeed, DC is conjugated to AB in both cases only because DA and DB have become two infinite lines. As we shall see, far from being the exception, this case in fact establishes the rule: that is, when D is projected at infinity, that very projection determines the harmonic ordering of the whole system.
So, to sum up. These ratios are crucial for two reasons: Firstly, because they tell us a great deal about the natural harmonic ordering of space, and most importantly that there is no such thing as “arbitrariness” in spatial relationships; and secondly, such ratios will tell us how far the movement of the soul must reach to access its principle, and will help us understand what we must seek in order to answer the question about our proportionality to the Infinite. But before going into that question, let us point out one thing that has to be addressed concerning the “complete quadrilateral.”
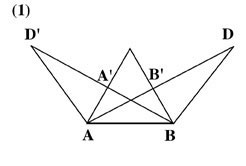
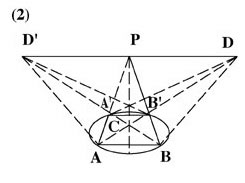
The complete quadrilateral is not simply what the Twentieth-century mathematician David Hilbert makes it out to be in his Geometry and the Imagination. In his Traité des Propriétés Projectives des Figures (Sec. II, Chap. I, Art. 154), Poncelet stresses that there is a difference between the simple quadrilateral (ABCD) and the complete quadrilateral (BAEDFCB) [See Figure 3], and this is, that the complete quadrilateral must have nine straight lines and as many harmonic ranges.
FIGURE 3
Simple quadrilateral ABCD and complete quadrilateral BAEDFC.
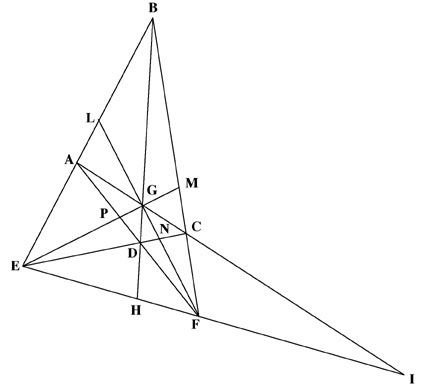
The nine harmonic ranges forming the complete quadrilateral are: EALB, EPGM, EDNC, EHFI, FCMB, FNGL, FDPA, BGDH, and AGCI.
Furthermore, Poncelet acknowledges that this theorem was known by the ancients, as it is reported by Pappus (Fourth century A.C.E. ) in his Collections Mathématiques, Book VII, Prop. CXLV, and that it was also reproduced by Grégoire de Saint-Vincent (Opus geometricum, Prop. X, 1647) and Laurent Lahire (Sectiones conicae, in Folio, Livre I, p. 5, 1685).
Sentiment of the Infinite
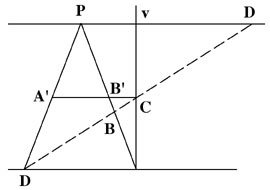
In Sec. I, Chap. I of his Traité des Propriétés Projectives des Figures, Poncelet establishes the fundamental theorem of projective geometry, which will represent a rigorous solution to Zeno’s paradox of the “bad infinite.” His theorem identifies what happens when the fourth point of a harmonic range ABCD, point D, goes to infinity, and establishes the basis for linear perspective, a perspective established by Leonardo da Vinci and Father Jean Pélerin Viator circa 1490 [See Figure 4].
FIGURE 4
Harmonic range ABDC, point D at infinity.
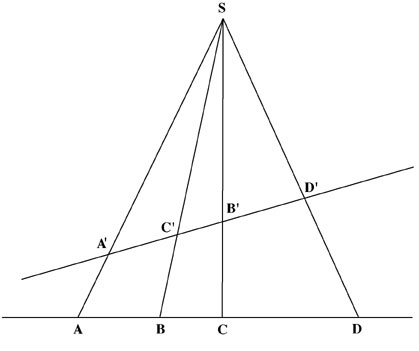
Suppose that point D is at infinity, or that SD is parallel to AB; segments DA and DB becoming simultaneously infinite, and differing from one another only by the finite quantity AB, shall have unity as their ratio, and consequently it shall be the same for CA and CB to which they are proportional: ... If two infinite magnitudes or distances differ from one another only by a given finite quantity, their ratio shall be unity; that is to say, they may be rigorously considered equal to one another.
The condition for Poncelet’s theorem to be true must flow essentially from the following two axiomatic considerations.
First, it is because the infinite ratio DA : DB corresponds to infinite unity, that CA : CB, a finite ratio, is reflected into a finite unity. And from this it must follow that all finite segments of equal partitioning of a perspective lattice shall have their receding scale formed everywhere by parallel lines.
Secondly, the partitioning of the perspective lattice into equal parts is consequent to the harmonic point D being projected at infinity; therefore the unity of the two infinite distances DA and DB, as well as their finite difference CA and CB, must be determined by the same projective property that establishes point D at infinity.
This theorem of Poncelet establishes explicitly, for the first time in history, not only that the harmonic range of the complete quadrilateral is nothing but the theorem of perspective, but also that the point at infinity, otherwise known during the Renaissance as the “subject point” (Jean Pélerin Viator), is a unique resolution of the Parmenides paradox of the One and the Many, and becomes the founding theorem of projective geometry.
From this, a more general theorem may be established, stating that if any number of infinite magnitudes or distances converge toward one point at infinity, they may differ from one another by some finite amount, but they cannot be affected in their cardinality by any changes in the lower finite order: that is to say, on the contrary, that it is the projective property of point D at infinity which determines the harmonic ordering of all of the finite and infinite distances of such a lattice. The point at infinity which determines an infinite number of such lines is thus a power point, which bounds every other point in the lattice from the outside, and is transfinite to them. This will become very important later for Cantor’s considerations in defining the transfinite numbers.
The reader should also note that this is what Lyndon LaRouche means, when he says that the higher species determines everything in the subordinated lower species, but that the lower species cannot determine anything with respect to the higher species. Indeed, this is surely the case where “poetry must supersede mathematics.”4
Lazare Carnot made this point very clearly in introducing the basic curriculum at the Ecole Polytechnique, where the science of “linear perspective” was to be superseded by the science of “aerial perspective,” where he says
[L]inear perspective ... is calculated mathematically, [but] aerial perspective ... can only be grasped by sentiment. By comparing these two sciences, where one is sensual, the other ideal, the methodical course of one will help penetrate the mysteries of the other. ... [Aerial perspective is] the art of generating ideas by means of the senses, of acting on the soul by the organ of vision. It is in this way that it acquires its importance, that it competes with poetry; that it can, like poetry, enlighten the mind, warm the heart, excite and nourish higher emotions. We shall emphasize the contributions that it can bring to morality and to government; and how, in the hands of the skillful legislator, it will be a powerful means of instilling horror of slavery and love of the fatherland, and will lead man to virtue.
Lazare Carnot,
from the “Drawing” section of the Public Works curriculum,
Ecole Poytechnique, 1794
The point is that unless you have reference to the infinite, harmonic ordering of the finite is not accessible.
Louis XI and the Institution
of the Nation-State (1461-81)
During the second half of the Fifteenth century, France became the theater of a very crucial experiment. Key players on one side included the Papacy, King Louis XI, his first Secretary Commynes, an uncertain but pivotal ally René II Duke of Lorraine, and the banking house of Medici, especially Lorenzo de Medici. Their objective was the creation of the nation of France. On the other side, were the Doge of Venice Giovanni Mocenigo, the dreaded enemy of France, and the leader of the “League” against Louis XI, the Venetian agent Charles the Bold, with a significant portion of the old aristocracy and medieval nobility, who wanted to maintain the old feudal order and their privileges over the abused population.
For over twenty years, Louis XI and his closest associates formed a strong alliance called the “League of Constance” involving several key duchies whose leaders remained faithful to the king. At the time, France had fourteen feudal duchies and ninety-four major cities, which Louis XI unified on the basis of the common good and of common development opportunities. This “commonwealth” idea was conveyed throughout the country in the slogan : “One law, one weight, one currency.” The king also established a unified, permanent army. Louis’ focus was to win the cities; to develop cultural centers, build manufactures, establish international trade fairs, and so forth, in order to attract talent from the rural areas (as well as from international quarters), to form a new political entity known as a nation-state. And indeed, the cities contributed wholeheartedly to guaranteeing this royal policy. But in order to unite the nation, the king needed the Duke of Lorraine, René II, a man who very much lacked a humanist education.
Worse than that, René II’s allegiance to the king was uncertain, as he was receiving 5,000 ducats a month from his alliance with Venice. So the king asked Father Jean Pélerin Viator, his secretary and confessor, to send Jean Ludovic de Pfaffenhofen, known as Jean Lud—the brother of Vautrin Lud, who later became the leader of the Vosges Gymnasium—to be René II’s ambassador and negotiator with the Doge in Venice.5 Jean Lud forged an agreement with the Doge, according to which René II would accept as enemies all the enemies of Venice, with the exception of the King of France.
On January 5, 1477, Charles the Bold, who reputedly had the largest army in all of Europe, gambled everything against the forces of France and its allies from Germany and Switzerland led by René II, and lost. On that day, remembered as the “Battle of Nancy,” Charles the Bold met a Shakespearean death which freed France to become the first nation-state. Today a modest bronze plaque composed by Viator can be seen on one of the pillars of the collegial chapel of Saint-George in Nancy, bearing the following inscription in memory of René II’s victory:
Ereptam patriam Dux ensifer ense recipit qui divina fovens juris armator erat. Viator(With the help of God, the Duke, fully armed friend of goodwill, has reunited the torn fatherland. Viator)During the very short period of a little over fifty years (1461-1510), Louis XI and his allies built the necessary educational institutions for the development of the nation-state, but they were unable to destroy their mortal enemy, Venice.
In 1509, the League of Cambrai brought together the largest military alliance ever put together against the Venetians, including Louis XII of France, the Emperor Maximilian I of Germany, Ferdinand of Aragon of Spain, Henry VIII of England, the Duke of Ferrara and the Medici bankers from Florence, and the instigator of the league, Pope Julius II. The military operations launched against Venice represented such overwhelming odds that it was nearly destroyed, forcing the Doge, Leonardo Loredan, to admit before the Great Council that their “sins of pride” and of “luxury” were being punished by God.
However, during the course of the same year, while negotiating for armistice and peace, the Venetian ambassadors succeeded in breaking the league by inducing Pope Julius II to quarrel with Louis XII and break the alliance. Conjuring the fears of a future conflict between a weak and divided Italy and a strong and unified France, the Venetian ambassadors succeeded in 1510 in convincing the Pope to lift the interdiction against Venice and form the Holy League with Venice against France. The fight to weaken and destroy the nation-state of France has been relentless ever since that period. Only the enduring character of the Platonic humanist institutions, such as the Brotherhood of the Common Life and the Oratorian Order, prevented a Venetian victory for so long.
During the short twenty-two year reign of Louis XI (1461-83), the most significant political change forced through by the king was to bankrupt the feudal landed aristocracy through the creation, and defense, of industries throughout France’s ninety-four cities, and through the opening of reciprocal trade with England and treaty agreements with Genoa, Florence, Naples, Sicily, and Calabria. Louis guaranteed the expansion of industries by subsidizing the cities, including the medieval cities; such subsidies came from taxations (la taille) which were inversely proportional to the productivity of the taxpayer. Accordingly, the feudal princes were more highly taxed than the townspeople, and the townspeople more than the city people. While salaries doubled during the reign of Louis XI, the total taxes collected on income tripled in the twenty-year period: the taille was 1,200,000 livres in 1462, and had reached the level of 3,900,000 livres in 1482. Whereas the majority of the people and cities never complained, the historical records are filled with complaints from the aristocracy, which had been frustrated in its privileges. In the ensuing fifty years, not one city ever turned against the king.
The crucial innovation, however, was the creation of new humanist schools and universities under the king’s authority. Louis XI presided over the establishment of the first Renaissance humanist studies, by creating two universities, one in Valence and the other in Bourges, in 1464. By 1471, he opened a printing house at the Sorbonne, and began the dissemination of Plato’s writings, as well as those of Sallustre, Virgil, Juvenal, and Xenophon (commissioned by the king himself). The Sorbonne press was Louis’ main propaganda tool in his denunciation of Charles the Bold; by 1477, the king had commissioned the first book in French, La Chronique by Saint-Denis, which narrates the actual building of the French nation from Roman times to the death of Louis’ father, Charles VII. Thus, the first French-language book was the history of how France became a nation!
It was a little after that period, that the city of Saint-Die, near Nancy in Lorraine, became a high point of the French Renaissance and one of the most important crossroads of humanist currents for the whole of Europe. Geographically situated on the routes between Strasbourg, Selestat, Heidelberg, Fribourg, Bale, and Paris, the small town of Saint-Die had established a Brotherhood of the Common Life school, the Vosges Gymnasium, which was actually an Academy in the sense of Leibniz, under the protection of both René II Duke of Lorraine, and the Vatican.
The Gymnasium was founded in 1490 as an ecclesiastic school directly under the control of Rome by Vautrin Lud, René II’s chaplain and brother of his ambassador to the Doge, and by Jean Pélerin Viator, then secretary to René II, and formerly secretary to Louis XI. It was staffed by the networks of the humanist school of Dringenberg from the Deventer school of the Brotherhood of the Common Life, students of the Alsatian humanist current of Geyser de Kaysersberg, friends of the mathematician Lefevre d’Etaples, and collaborators of Leonardo da Vinci and Pico della Mirandola in Italy.
Aside from being a “Latin school” in the tradition of the Brotherhood’s “devotio moderna,” the Vosges Gymnasium ran an important printing house for the dissemination of scientific works in geography, music, and geometry. Its first publication was a treatise on perspective (De Artificiali Perspectiva, 1505) by Jean Pélerin Viator, published both in French and Latin. Viator’s treatise not only represented the very first treatise on perspective to be published in Europe (the works of Alberti, Piero della Francesca, Filatere, Foppa, and Leonardo da Vinci were highly controlled by oligarchs, and only circulated in manuscript form at the time), but it represented a completely original Platonic approach to the application of perspective to city building. The Vosges Gymnasium also produced the first world map published by Mathias Ringmann which identifies the entire continent of South America [See Figure 5].(not available)
After the first edition of Viator’s book, there would be no less than five pirate editions in Germany from 1508 to 1535, and three editions in France from 1505 to 1521. The perspective conception would greatly influence the great French painter Jean Fouquet, and Albrecht Dürer would demonstrate the Viator construction in his “Saint Jerome” (1514). But by the time that Jacopo Barozzi da Vignola, who knew Viator’s work very well, wrote his Due Regule della Prospettiva Pratica (1583), Viator’s name was all but forgotten. In fact, by that time, the word “Viator” no longer appeared as the author, but as the title, of his book—an error made possible by a French pun on the word “viator.” But, even though the author could be erased from the historical record, the idea could not be stopped. But why? What was so dangerous about Viator’s “perspective”?
Viator writes at the opening of his book that this knowledge will “elevate the observers’ minds” and will “transport their hearts toward virtue and Divine action,” because perspective has the ability to “console and transcend the sorrows of human life.” That is why the Venetians had to keep this method of developing the human mind away from the general population. Vignola will later say that Viator’s perspective is easy to apply but “difficult to understand” [See Figure 6].
FIGURE 6
Perspective diagrams from Viator’s De Artificiali Perspectivea” (1505).
(Reprinted from L. Brion-Guerry, “Jean Pérerin Viator,” by permission of the publisher.)

This is also the objective that Monge and Carnot would assign as the crucial function of perspective, to develop in the students the sentiments of elevation, of proportionality, and of the infinite—that is, the movement of the soul through which noble thoughts, such as the ideas of creativity, inalienable rights, the Good, Truth, Beauty, love of God and love of mankind, and so on, can be developed. In other words, perspective, properly understood, is a “higher species” than linear proportion, and it will develop political freedom in a people.
By 1642, Viator’s perspective would have a determining impact on Gérard Desargues. Desargues became embattled over the issue with a Jesuit Father Du Breuil, who not only plagiarized Viator in his book La Perspective Pratique (1642), but would also later plagiarize Desargues’ work in projective geometry. A very nasty fight ensued, which would last until 1661, when Desargues’ publisher Abraham Bosse, himself an expert in perspective, was expelled from the French Academy by the Jesuits. Thus have the works of Viator, Desargues, and Bosse been pirated, distorted, plagiarized, and kept hidden for over 500 years, until today.
Desargues’ Theorem (1639)
The usual textbook presentation of “Desargues’ Theorem” states that, given two triangles ABC and A′B′C′, whose corresponding vertices converge toward vertex D of a pyramid, it follows that if you project the three pairs of corresponding edges two by two, they will intersect at three points E,F,G which lie on a straight line, as is shown in Figure 9. This formulation—which is unlikely to reflect the original theorem of Desargues—does not give the full scope of what is implied in its discovery, however, as is demonstrated by the following construction:
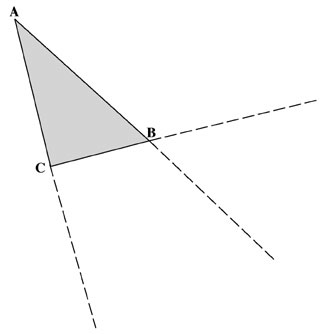
First, trace any triangle ABC and extend its three sides in the same direction, as shown in [See Figure 7].
FIGURE 7
Triangle ABC
Second, intersect the three extensions with a straight line EFG anywhere, to form an ordinary quadrilateral ACGFEBA [See Figure 8].
FIGURE 8
Quadrilateral ACGFEB
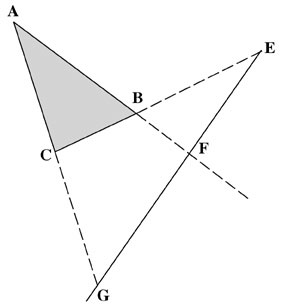
Third, project from a point D three rays DA, DB, and DC, onto another plane A′B′C′ along the extensions of these rays. This new plane of triangle A′B′C′ intersects the plane of triangle ABC at the fold EFG, the axis of rotation of the whole system [See Figure 9].
FIGURE 9
Desargue’s Theorem construction
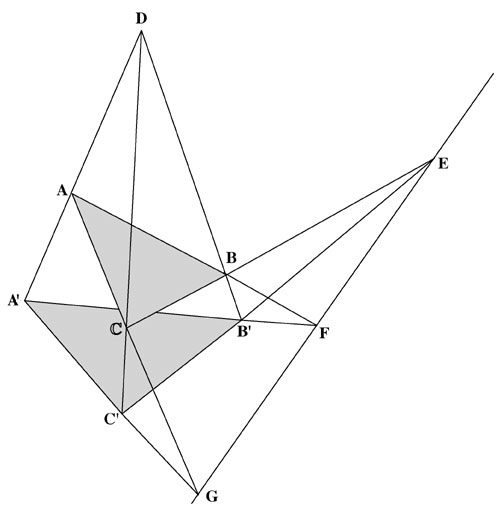
This Desargues construction, in its simplest descriptive expression, presents the interconnectedness of five ordinary quadrilaterals; that is, the rotation around an axis EFG of a quadrilateral ACGFEBA, whose shadow quadrilateral A′C′GFEB′A′ is projected from point D. The connection between these two ordinary quadrilaterals and point D will form three other quadrilaterals: (1) DAA′C′GCD; (2) DAA′B′FBD; and (3) DCC′B′EBD.
The crucial point about this theorem is that it is a continuation of Nicolaus of Cusa’s notion of the trinitarian principle of action in the universe. More specifically, this construction is built on the principle of triply-self-reflexive conical action of the three-point perspective of Viator [See Figure C.2, In “Solving the Paradox of the One and the Many” Box ], and will become the paradigm for all of projective geometry, including the harmonic ordering of the complete quadrilateral as Poncelet later defined it [See Figure 3].
FIGURE 3
Simple quadrilateral ABCD and complete quadrilateral BAEDFC.

In this theorem, Desargues establishes implicitly two things. One is that geometry must be constructive or synthetic (as opposed to analytic); that is, following in the footsteps of the Greeks—for whom everything had to be constructed with a compass alone—everything here must be constructable with a straight edge alone. And second, the theorem establishes the basis for the harmonic ordering of both geometry and music, as will be indicated in the following theorems of Pascal, Poncelet, and Monge.
The Pascal Theorem (1645)
At the early age of sixteen, Blaise Pascal, under the guidance of his teacher Desargues, had already elaborated his main contribution to geometry, which came to be known as the “Essay on Conics.” He is known to have derived over a hundred theorems, covering virtually a complete treatise on conics, which is lost today. Leibniz himself insisted that this treatise be published by Pascal’s nephew Perrier, but it was never done, and this crucial work has never reached us. The precious treatise had been kept hidden or destroyed by the networks around the chief Venetian agent in France at the time, Descartes, who hated synthetic constructive geometry with a passion.
Although tremendous discoveries in the domain of constructive geometry were achieved in the Seventeenth century through the collaboration of Leibniz, Huyghens, Fermat, and the Bernoulli brothers in the domain of transcendental or non-algebraic curves such as cycloids,6 which Descartes also attempted to obfuscate, the loss of Pascal’s work was no doubt the crucial factor in retarding the development of projective geometry for another 150 years, until the breakthroughs of Monge and Carnot in 1794.7
One of the most fruitful theorems of Pascal, known also as the Hexagrammum Mysticum, states that when you inscribe a hexagon formed by six points A,L,B,D,N,C in a conic, the three points of intersection Q,G,P of opposite sides lie on a straight line [See Figure 10].
FIGURE 10
Pascal’s Hexagrammum Mysticum.
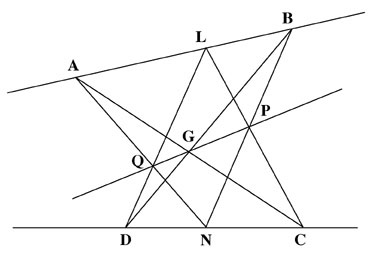
The projective property which establishes this “Pascal line” is the same as that which determines the fourth side of the quadrilateral in the three-point perspective of Viator.
This theorem further suggests that Pascal might have known about the harmonic range of the complete quadrilateral. Compare the Pascal hexagon with the Viator device for perspective A,L,B,N,C [See Figure: 11].
FIGURE 11
Viator perspective device (see Figure C.2)
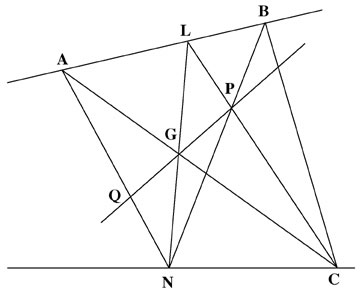
Note that by only modifying a few lines in the general correlation of the hexagon of Pascal, you have transformed the original figure into a different one, a pentagon; the two figures are composed of the same number of lines but they are disposed in a different manner in each case. What this does, is change the theorem, without changing the projective characteristics of the figures; both figures retain absolutely the same projective properties. This is what Poncelet identified as discontinuities within the constraint of the principle of continuity.8
Similarly, although the theorems of the complete quadrilateral are somewhat different from the theorems of conic sections, the principle of generation of both is the same; this will be the case every time a figure can be derived from another figure by simple change of configuration or transposition of certain parts, and without affecting the generative principle underlying them.
The profitability of such exercises lies in the discovery of the valid crucial transpositions or changes which may be construed by pushing the system of theorems to their limit. It is by this means that one can discover crucial discontinuities that call into question the generative principle from which they are derived, and lead the mind to seek the next higher truth of a new and more universal generative principle.
A similar result may be obtained by bridging the non-linear gap between three- and two- dimensionalities. A beautiful case of Nicolaus of Cusa’s Trinity of Unity, Equality, and Connection, can exemplify this by an extermely elegant theorem of Poncelet, which states that “from the same point, on the same line, and in the same direction, you may trace three distances such that the first minus the second is to the second minus the third, as the first is to the third” [See Figure 12].
FIGURE 12

This implies a jump between the harmonic divisions of three-dimensional space, and the equal divisions of parts in the two-dimensional plane! This is the very same harmonic division which forms the basis of the well-tempered musical scale, that is, the relationship between the three fundamental intervals: the octave, fifth, and fourth. Another way to formulate this is: the ratio of the octave divided by the ratio of the fifth, is equal to the ratio of the fourth.
Now, suppose that the first of these three distances, AD, is infinite; it will suffice to show that because this infinite projection is the generative principle of the harmonic proportion [See Figure 4],
FIGURE 4
Harmonic range ABDC, point D at infinity.

the three segments will correspond to equality of unity! This signifies that the harmonic divisions of a line are nothing but an extension of the division in equal parts of an infinite line. This is a most elegant way of discovering the Uniqueness of the transfinite and how it harmonically subsumes the Many. You can locate this in the construction shown in Figure 13.
FIGURE 13
The harmonic divisions of a finite line are nothing but an extension of the
division in equal parts of an infinite line.
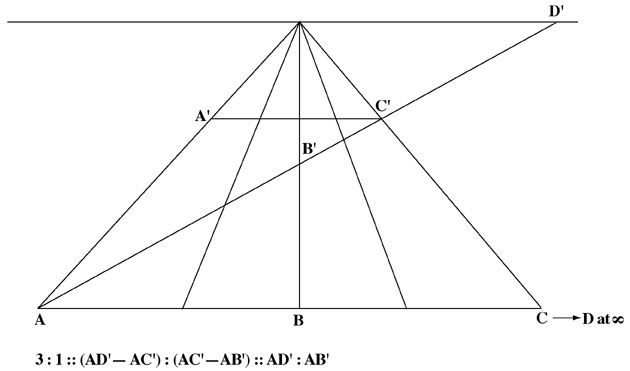
Point D′, being at infinity on the receding three-dimensional scale of AB′C′D′, correlates with point D, which is at infinity on the infinite two-dimensional line ABCD, because the equal division of AB : BC is to AD : CD, as the harmonic ordering on the traversal range of AB′ : B′C′ is to AD′ : C′D′, that is, as the one infinite is to the triune.
The Poncelet Principle of Continuity (1822)
One exquisite case is a theorem of Poncelet which brings all of this together very nicely, and exemplifies beautifully the LaRouche model of an aleph in a projective form. First refer yourselves to LaRouche’s construction of the aleph model, and locate this primary figure, as he draws it, and extend the sides of the polygons in parallel lines [See Figure 14(a)].9 The inscribed polygon ABCD and the circumscribed polygon abcd are of two different and lower species with respect to the circle. No matter how many sides you add to the polygons, they will never coincide with the circle. Now, transform the LaRouche model into a Poncelet projective model [See Figure 14(b)]:
FIGURE 14 (a)(b)
The harmonic divisions of a finite line are nothing but an extension of the
division in equal parts of an infinite line.
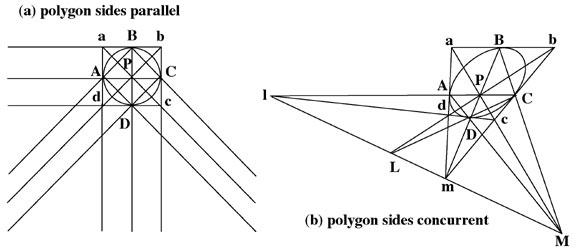
If you inscribe inside of a conic section a quadrilateral ABCD, and circumscribe it with another abcd in such a way that the sides of the second touch the curve at the vertices of the first: [Poncelet derives five considerations, of which we present only the fifth] (5) All the straight lines going through point P and ending at the conic section or at two opposite ends of each of the quadrilaterals, will be divided harmonically at that same point and at the one where the straight line meets its polar LM; similarly with points M and L with regards to lines PM and PL of which they are the poles.
—Jean-Victor Poncelet,
Traité des Propriétés Projectives des Figures,
Vol. I, Sec. I, Chap. III, Art. 186
To bring together the two- and three- dimensionalities, Poncelet had to discover a determinable infinite, closure, which would resolve the paradox of parallel lines meeting in a point at infinity; this paradoxical concept shows how all of the eight sides of the polygons and the four diagonals meet on one finite line at four harmonically ordered finite points. This theorem expresses the underlying axiomatic principle of continuity between the two-dimensional parallel system and the three-dimensional concurrent system, orthographic and perspective projections. Indeed, the theorem resolves the paradox whereby parallel lines meet at infinity in a single point, an infinite point which is interchangeable with a finite point on a finite line by means of projection. We shall soon see how Monge resolves this same paradox in a different way.
Consider, lastly, that the curvature of physical space-time developed later by Bernhard Riemann (1826-66), would be derived directly from Jacob Steiner (1796-1863), whose entire work was inspired by these Poncelet projections.
Jacobins vs. Girondins, or the Power of Reason
Let us take, for a moment, another paradox that results from the apparent conflict between man and nature: nature always attempting to subjugate man, and man always trying to dominate nature. If nature were to succeed in dominating man, then man would be reduced to a mere beast, and nature would become pure multiplicity, pure heteronomy; no unity could ever exist and everywhere nature would be pure chaos and disorder. This is the state of affairs that chaos theory is pushing today. And since animality does not have within itself the principle of its own unity, there must be a higher species—man—which must provide that unity of determination.
The question therefore arises, as to how man can be reconciled with nature: how do you conserve the multiplicity of nature with the moral unity of man, how do you resolve, again, that paradox of the One and the Many? You solve that paradox by introducing technology into nature, and civilization then comes to be, to the extent to which man becomes able to master and subdue the environment by improving technological innovations. Thus, science and technological progress become the means by which man is able to reconcile his moral unity with the multiplicity of nature, and to transform nature for his own benefit according to the injunction of God to “be fruitful, multiply, and have dominion over nature” (Genesis 1:28).
In this way, man is no longer condemned to hard labor, no longer made to fight against nature like an animal to survive. Man does the intellectual work, while nature does the laborious work: thus, man must do the work of the One, by developing his creative reason and applying it to nature, while nature must do the work of the Many, by applying human technology. That is the way the creation of the Ecole Polytechnique was able to solve the paradox of the One and the Many.
The important point to be made here, is the fact that the French Revolution of 1789 was actually a counter-revolution led by a mob of “enragés” who were led to destroy three hundred years of science and technology that had been painstakingly developed by the Brotherhood of the Common Life and by the Oratorian teaching order.
And so, Gaspard Monge and Lazare Carnot had to find a solution to the urgent crisis that was causing terror throughout France from 1789 to 1794—a crisis that had been orchestrated by the British/Swiss agent Jacques Necker, by manipulating and dividing French society into two camps, the Jacobins represented by Marat, Danton, Robespierre, and their theoretician, Jean-Jacques Rousseau, and the Girondins represented by the royalists, the Jesuits, and such leadership of the aristocracy as Voltaire. This was the conflict rigged by the London Venetian Party of Shelburne, King George III, and their head of British intelligence, Jeremy Bentham, the conflict between savages and barbarians that was to pit pure, uncontrolled “emotions” (pure heteronomy) on the one side, against soul-less pure “reason” on the other. Such was the paradox that the leaders of the Ecole Polytechnique worked to solve—as expressed by Carnot in his beautiful poem—by fostering “enthusiasm” for scientific discoveries:
| Ode to Enthusiasm
by Lazare Carnot Sublime soaring of generous souls, |
Ode a l’enthousiasme
par Lazare Carnot Sublime essor des grandes âmes, |
Schiller also had a very concise description of this French Revolution, which he called “A great moment which found a small people.” This is how he refers to the situation in his “On the Aesthetical Education of Man,” especially the end of Letter IV:
Man can, however, be opposed to himself in a twofold manner: either as a savage, if his feelings rule over his principles, or as a barbarian, if his principles destroy his feelings. The savage despises art and recognizes nature as his unrestricted master; the barbarian derides and disrespects nature but, more contemptible than the savage, he frequently enough continues, to be the slave of his slaves. The educated man makes nature into his friend and honors its freedom, while he merely bridles its caprices.When reason therefore brings her moral unity into physical society, she should not damage the multiplicity of nature. When nature strives to maintain its multiplicity in the moral structure of society, there should be no breach in the moral unity; equally far from uniformity and confusion rests the victorious form. Totality of character must therefore be found in the people, which should be capable and worthy, of exchanging the state of necessity for the state of freedom.
—Frederich Schiller,
“On the Aesthetical Education of Man,” Letter IV
And since the Jacobin terror had destroyed the laboratories and guillotined the scientists (such as Lavoisier), there was no better and more necessary idea than to establish a curriculum based on geometric discoveries, as the catalyst that would lead to the discovery of the creative process of the human mind, and give France the scientists, the engineers, the metallurgists, the chemists, and so forth, that the nation-state needed so desperately. And so began the real French Revolution when, in 1794, Robespierre was defeated by Carnot, and the Committee of Public Safety passed a resolution for the creation of the Ecole Polytechnique and the Ecole des Arts et Métiers [Arts and Trades]. As Poncelet, one of the very first student brigade leaders would later express it,
We do not intend to teach you a method and a process for each art, but instead what is the principle common to all of the arts ... with the purpose of making inventors out of you, inventing new machines and new processes.Just as life gives the body its unity, projective and descriptive geometry brought to national education its vital inspiration, without which all of the arts and scientific studies would have been disparate and meaningless. In fact, national French education was organized around this unifying geometric idea, according to which students were required to master the underlying principle of a given discipline, then apply the same underlying principle to another discipline, and lastly embrace in a unique theorem the principle underlying all of the disciplines of human industry. Such a higher geometric principle is what Poncelet formulated as the basis for the development of arts and crafts throughout France, “this principle of continuity which broadens the mind and embraces in a unique theorem a multitude of lesser truths.”
Perspective and projective geometry, which had been the exclusive science of painters and of cathedral builders up until that time, now became the very foundation of the industrial revolution. Monge would apply the principles of projective geometry to the design and manufacture of standardized and interchangeable parts for military components. From then on, everything that had been previously built by hand had to be recast at the foundry, based on uniform and universal designs that would become the standard for each and every small part of an assembly, from a simple mechanical wheel, to a complicated piece of artillery, to a ocean-going vessel; the kinds of machinery designs that Leonardo da Vinci had developed three hundred years before, now became the standard type of models for the Ecole Polytechnique [See Figure 15].
FIGURE 15
Principles of projective geometry applied to machine design (orthographic projection). (a) Leonardo da Vinci, “Machine for making bands of copper,” Manuscript G, 70v. (not shown) (b) Modern machine design, as standardized by Monnge at the Ecole Polytechnique.
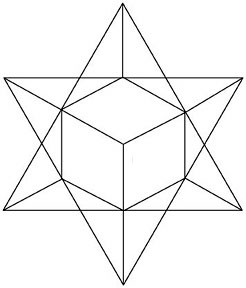
Correlate this with the geometry of Kepler’s snowflake principle of close-packing, this cubic projection which is inscribed in the dodecahedron [See Figure 16].10
FIGURE 16
Cubic projection. Close-packing, as described by Kepler in “The Six-Cornered
Snowflake,” derives from the properties of the dodecahedron.
There is only one way to map all of the points of a three-dimensional object onto a two-dimensional plane, and that is to discover the means of triply relating pairwise (biunivocal) relations as one. This is what the dodecahedron generates in the form of the inscribed cube when you unfold its sides onto a two-dimensional plane [See Figure 17(a)].
FIGURE 17
Orthographic projection. (a) Unfolding a dube onto a two-dimensioinal plane. (b) Three -dimensional object represented orthographically in two dimensions.
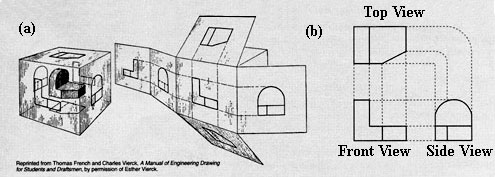
Monge would affix the different views of the orthographic projection, in the same plane. The idea was to completely represent every aspect of a three-dimensional object on a two-dimensional plane. This was done such that perpendicular lines drawn in each of the three planes of projection, are all orthographically interconnected into one single projection of (1) the frontal view; (2) the top view; and (3) the side view, as in shown in Figure 17(b).
This is done by a simple circular generative process of unfolding the different sides, whose interconnectedness is extended by parallel projective lines falling at right angles to one another. The projective angles of 120° in one domain correspond to right angle (orthographic) projections of 90° in the other. If you complete the projections of the rear, bottom, and left sides of the cube, you will have gone full circle, that is, you will have covered the six sides of the cube, or the complete sphere.
The crucial point here is that the horizontal and vertical magnitudes of a two-dimensional plane are able to contain all three dimensions of an object, provided that one can discover the unique way to relate triply, as one all of the dual relations: (1) height and width; (2) width and depth; and (3) depth and height. If these relationships taken two by two can, together, form a unity of all three variables, then you have an equivalence of relations between volumes and planes. This means that the principle which defines the ordering of the triple relation is of the same species as that which determines the duality of relationships.
Consider, however, that the ability to project such a three-dimensional object onto a two-dimensional plane is not a simple task to realize. It is not the trivial action of measuring something forward, upward, and sideways, or simply filling “linear extension” in all directions. It is not a simple act of adding a new “dimension” to a surface; you are not simply going from the square to the cube. What you are dealing with is an actual unity of reflection of the creative process, of the faculty of imagination (of which, by the way, animals are not capable), in the sense that you are projecting on a lower manifold the geometry of a higher manifold, which involves the creation of a leap caused by the generative principle of a One, a common principle, which underlies an infinity of space-connected problems, and bounds them together from the outside.
Again, that One is exemplified by the generative principle of the Viator three-point perspective. It is from this vantage point that Monge would develop his descriptive geometry, which would lead to developing the generative principle of orthographic projection for industrial design. But in his classes, Monge would make use of only two planes of projections, since the horizontal and the vertical projective planes are sufficient to convey the three dimensions.
Thus, the principle of this parallel projection does not lie in the connection between points, lines, and surfaces, as such, but more fundamentally in the ability to access and discover the region of the mind which foreshadows the higher characteristic between two distinct manifolds rather than concentrating on the variable positions of the perceived objects from one manifold or the other. This is not a question of Aristotelian reduction to sense perception, but of a Platonic approach to knowledge.
of Projective Geometry
(Viator, Desargues, Pascal, Monge, and Poncelet)
Let us take the example of a series of theorems which represent a historical sequence of “predecessors” and “successors” in isochronic collaboration with one another over a period of over three hundred years. (The term “integral” here is not used in the usual analytical sense of the word, but more broadly, meaning that the theorems of Viator and Desargues actually integrate, synthetically, the theorems of Pascal, Monge, and Poncelet, into one single Viator-Desargues Integral Theorem of projective geometry.) First, the Poncelet complete quadrilateral with its nine integrated harmonic ranges (Figure 3) is derived from the Monge Four-Sphere Theorem (Figure 18), which itself is derived from Desargues’ Theorem (Figure 9). In turn, you could easily find that Desargues’ Theorem is itself derived from Viator’s three-point perspective. Hence, a series of crucial theorems initiated from the Viator-Desargues Integral Theorem determines Euclidean geometry essentially as the science of projective synthetic geometry.11
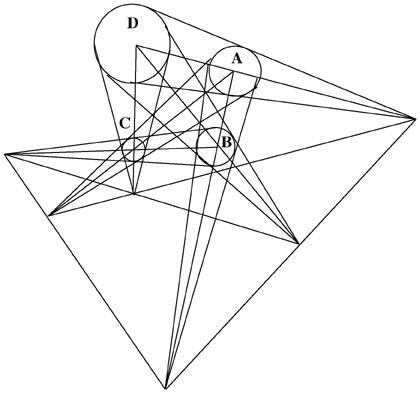
The Monge Four-Sphere Theorem
Given four spheres (A,B,C, and D) of different positions and size in space, if you conceive of six conical surfaces which circumscribes them externally, two by two, the summits of these six cones shall be in the same plane and at the intersections of four straight lines; and if you conceive of six other conical surfaces, circumscribed internally (that is to say, which have their summits between the centers of two spheres), the summits of these six new cones will be, three by three, in the same plane with three of the first ones [See Figure 18].
—Gaspard Monge
FIGURE 18
Monge Four-Spere Theorem construction.
The same principle of continuity may be pursued in the case of packing of spheres in space, such that, for every three spheres of different sizes and positions in the plane which are enveloped by conic surfaces whose three apexes fall on the same straight line, there exists a fourth sphere whose center forms, with the centers of the three other spheres, and with the internal and external points of similitudes, nine harmonic ranges belonging to a complete quadrilateral in one single plane. This plane is one of the five such planes that form the Viator-Desargues Integral Theorem construction [See Figure 19].
FIGURE 19
Viator-Desargues Integral Theorem construction (shnowing only a single plane.
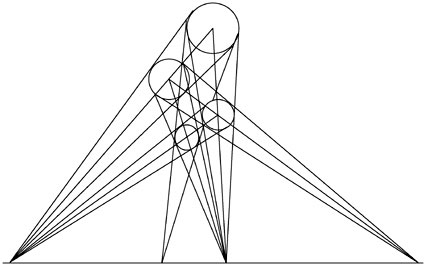
It can be further demonstrated that, for every three spheres of different size and position, there exists a fourth sphere which lies in the same plane and is conjugated with the other three to form a harmonic quadrilateral. The positions of the four spheres relative to one another, (or of the same sphere rotating along an elliptic path to different positions), are harmonically ordered in the plane, just as the four external points formed by the apexes of their circumscribing cones are harmonically ordered on a straight line.
Since each plane of three spheres of different size and position can have a fourth sphere (Figure 19) which is harmonically conjugated to the three others to form a harmonic cluster, the completed form of the Desargues, Pascal, Monge, and Poncelet Theorems will reflect a harmonic field.
Thus, all of the spheres of the Viator-Desargues Integral Theorem will form a harmonic field of clustered spheres which, in Poncelet’s terminology, will correspond to the continuous projective property of five complete quadrilaterals generated by multiply-connected circular action onto five different planes (including ten straight lines and ten harmonic ranges); or, in Monge’s terminology, ten conical projections tangent to eight spheres of different sizes and positions in space, oriented two by two, and forming through their internal and external centers of similarity, ten harmonic ranges. (Figures 20 (a) and (b) shows the Viator-Desargues Integral Theorem with only four spheres.)
FIGURE 20
Three-dimensional representation of the Viator-Desargues Integral Theorem construction. (a) Four-sphere model. (b) Eight-sphere model.
 |
 |
Synthetic Geometry vs. Algebraic Analysis
This transformation, this higher form of correlation between theorems, corresponds to what Carnot called “natural geometry”—as opposed to algebraic analysis, which cannot make such non-linear correlations. This is why Baron Augustin Cauchy, the “father of analysis,” eliminated such basic constructions from the curriculum of the Ecole Polytechnique. Now, this historical sequence of discoveries by geometers contributed to the crucial breakthroughs which brought about the development of every major discovery of the industrial revolution. So you have here, in essence, the crux of the conflict between the Aristotelian/Venetian method and the Platonic method.
If Cauchy had been an honest analyst, he would have had to admit that one cannot make the leap from the side to the diagonal of a polygon at infinity, the place where rational and irrational numbers meet on the same line. No matter what open-endedness you may find in the two-dimensional plane, you will nonetheless find closure in the three-dimensional magnitude, by virtue of the generative principle underlying the Viator-Desargues Integral Theorem. This is why Cauchy didn’t understand the Poncelet principle of continuity, and despised it.
This synthetic-constructive method of “natural geometry” can only be understood, wrote Carnot in his “Eloge de Vauban” (1783), by means of “principles which are, so to speak, located in le sentiment,” as opposed to algebraic analysis, which can only be acquired by memorization of formulas. Indeed, synthetic-constructive geometry aims at elevating the soul through noble emotions, such as passion for scientific discovery, or love of God and love of mankind, by means of discovering non-linear correlations between entities which otherwise have no “algebraic” relationship whatsoever. This is why synthetic geometry is useful for innovation, but algebraic analysis is not.
The algebraic-analysis approach, on the other hand, is (as described here by Carnot) an “abstract art of building systems, the art of tracing on paper lines which are dependent in their mutual positions on quasi-arbitrary conditions to which some people have given the important name of axioms.” It may be acceptable for an engineering task, but it is useless for the purpose of invention; in fact, it is detrimental to the creative process.
Ultimately, algebraic analysis will lead you easily to cultural pessimism, because it is a region of dry, passionless, deductive processes which stultifies creativity. Its main claim to fame is cold, logical proof, which its sycophants elevate to the supreme level of the elitist knowledge that they portray as science. Just to give you a taste of this pessimism, witness how Baron Cauchy himself, a Bourbon “legitimist” and a sworn enemy of Poncelet, conceived of the importance of human discovery:
When we take a quick look at the productions of the human mind, we are tempted to believe that human knowledge can grow and and multiply itself at infinity. ... However, if we observe that all of our intelligence and our means are enclosed within limits that can never be superseded, we will persuade ourselves that our knowledge is limited ... that if man has been unable to visit the poles, he remains in an eternal despair of ever reaching these frozen regions ... . Who will ever be able to dig a well of 1,500 leagues deep? We have managed to elevate ourselves to 1,500 fathoms in the atmosphere, but the rarity of the air ... will constantly bring back to earth’s surface whomever would want to reach higher ... . Exact sciences can be considered as completed sciences ... . By means of sophisms man can come to the point of doubting these truths we teach him, but he will never discover new ones!
Augustin Cauchy, Cherbourg, 1811 Such a spirit of limitation can come only from a prolonged contact with the oligarchical worldview, the view of man as an animal, and the algebraic method itself, which is defined internally from the very limitations of the axioms and postulates which generate theorem-lattices. So, by virtue of the very nature of the closed completeness of theorem-lattices, it is impossible for an algebraic-animalist mind to make the non-linear leap between sets of theorem-lattices; which is what is required for creative discoveries.
Enthusiasm: The ‘Inner God’
It was Louis Pasteur who continued the spirit of the Ecole into late-Nineteenth century France. He saw very clearly the acute crisis that France had been going through since 1815, and he identified precisely the problem that had crippled the nation since the Congress of Vienna. The joy of discovery had been killed in the school system, and the “inner God” (as he put it, recalling Carnot’s commitment to “enthusiasm”) was no longer the praised emblem and principle of the Ecole. It had been replaced by the evil of radical positivism.
By 1814, Auguste Cauchy and Auguste Comte had taken over the Ecole Polytechnique and had totally subverted its high purpose.12 They dumbed-down everything to what became known as Positivism, the “new religion of man”—what was later called “secular humanism.” This was the context for the following beautiful statement of Pasteur:
Positivism sins not only through methodological error. There is a considerable gap in its seemingly tight net of reasoning ... . The large and obvious flaw in the system consists in that the positivist conception of the world does not take into account the most important of positive notions—that of the infinite.What lies beyond the starry vault of the heavens? More starry heavens. So be it! And beyond? Pushed by an invisible force, the human mind will never cease asking itself: What is there beyond? Does it want to stop either in time or space? Since an endpoint would be merely a finite dimension, greater only than those that had preceded it, no longer does the mind begin to envision it than this implacable question returns, and the mind cannot quell curiosity’s call. ... Positivism gratuitously brushes aside this positive and fundamental notion, along with its consequences for the life of society. ...
Are not the science and passion of understanding nothing else but the effects of the spur of knowledge, put in our souls by the mystery of the universe? Where are the real sources of human dignity, of liberty and of modern democracy, if not in the notion of the infinite before which all men are equal.
The spiritual bond situated [by the positivists—PB] within a sort of lower-level religion of Man, cannot reside elsewhere than within the higher notion of the infinite, because this spiritual bond must be associated with the mystery of the world. The Religion of Man is one of those superficially obvious and suspect ideas which brought one eminent psychologist to say : “I have thought for a long time that the person who has only clear and precise ideas must assuredly be a fool. For the most precious notions harbored by human intelligence are deeply behind-the-scene and in semi-daylight, and it is around these confused ideas, whose interrelations escape us, that the clear ideas gravitate, extending, developing, and germinating themselves.” If we were cut off from this background, the exact sciences would lose the greatness which they draw from the secret rapport they hold with those infinite truths whose existence we can only suspect.
The Greeks understood this mysterious power below the surface of things. It is they who bequeathed to us one of the most beautiful words of our language: the word enthusiasm, [which means] “inner God.”
The greatness of human actions is measured by the inspiration that gives them birth. Joyous is he who carries within him an inner God, an ideal of beauty, which he obeys: an ideal of art, an ideal of science, an ideal of his nation, an ideal of the virtues of the Gospel. These are the living sources of great thoughts and great actions, and all of them are lit by the gleam of the infinite.
—Louis Pasteur,
Speech delivered to the French Academy of Sciences, 1882
The Leonardo/Viator Method:
|
||||||||||||||||
|
||||||
On the foreshortening of the square circumbscribed by a circle, Jean Pélerin Viator established in his De Artificiali Perspectiva, that perspective is based on a triply-self-reflexive rotation of intersecting visual pyramids, an approach typical of Leonardo. With the three apexes of the three cones located on a straight line representing the infinite horizon, Viator’s theorem reads:
The narrowing of the receding square lying in the plane A,B,B′,A′ is constructed from the inclined radial lines of the central visual pyramid P, which intersect two other visual pyramids projected from third points D and D′, which are equally removed from the subject point P at a distance twice the width AB of the tetragon, or more or less that distance depending on the closer or farther view. And the circle circumbscribing the square is generated from the sphere, and is perceived inclined as an oval or as a lens depending on the position of the frontal view.
—Jean Pélerin Viator,
De Artificiali Perspectiva, Fol. 5
Although no document attests to Leonardo’s or Viator’s explicit knowledge of the harmonic range as later developed by Poncelet, both based linear perspective on a harmonic ordering of the complete quadrilateral, where AD : B′D :: AC : CB′. (Viator’s above-mentioned relationship PD = PD′ = 2AB = 2/1 is derivable from the generative principle of the Golden Section of the dodecahedron.)
back to article

1. In the French tradition, sentiment is used to mean the emotion of agape that is conjoined with the activity of creative reason. This has nothing to do with “feelings” per se, referring instead to the higher emotions, such as freedom, love of God, love of country, and everything that relates to the common good of mankind as opposed to “personal” interest. For an extended discussion of this question, see Jacques Cheminade, Régard sur la France républicaine (Paris: Editions Alcuin, 1991).
2. Cf. Lyndon H. LaRouche, Jr., “On the Subject of Metaphor,” Fidelio, Vol. I, No. 3, Fall 1992, pp. 36-39.
3. We use the mathematical notation for expressing ratios and proportions, rather than the more familiar arithmetic notation DA / DB = CA / CB, because the former denotes geometrical relations, whereas the latter denotes algebraic ones.
4. Cf. Lyndon H. LaRouche, Jr., “The Fraud of Algebraic Causality,” in “Symposium: The Creative Principle in Art and Science,” Fidelio, Vol. III, No. 4, Winter 1994.
5. For the life of Viator, see L. Brion-Guery, Jean Pélerin Viator (Paris: Les Belles Lettres, 1962).
6. Cf. Lyndon H. LaRouche, “Metaphor,” op. cit., pp. 23-36.
7. It should be noted that even the current scholarly literature, such as the Source Book in Mathematics of David Eugene Smith, continues to this day the same Venetian tradition of mistranslating and disfiguring the few remains of Pascal’s work, as exemplified by certain unintelligible translations of his theorems. David Eugene Smith, A Source Book in Mathematics (New York: Dover Publications, 1959), pp. 326-330.
8. Dino de Paoli, “Construction of a Harmonic Golden Section,” Leesurg, 1978 (unpublished).
9. Cf. Lyndon H. LaRouche, Jr., “Metaphor,” op. cit., Figure 1, p. 19. The author has chosen to term LaRouche’s diagram the aleph model, as it illustrates the first of the successive levels of the mathematical transfinite of Cantor’s aleph series.
10. Johannes Kepler, De Nive Sexangula (On the Six-Cornered Snowflake), trans. by Colin Hardie (Oxford: Clarendon Press, 1966; reprinted by 21st Century Science & Technology, 1991).
11. The author has shown elsewhere that the construction represented by this Integral Theorem is actually bounded by the dodecahedron, as the underlying “One of the Many” which Raphael Sanzio used as the architectonic idea for his “School of Athens” fresco. Although this discovery cannot be presented here, the reader should know that all theorems of dodecahedral Euclidean space, be they of finite or infinite magnitude, find their generative principle in the boundary conditions set from the outside by the nested projection of an icosacuboctadodecasphere, which represents a higher geometry from the standpoint of the Keplerian quantum field.
12. A Note on Polytechnique and America. As early as 1815, the Congress of Vienna forced the expatriation of the Polytechnique method into Germany and the United States, where two polytechnician students Claude Crozet and Isaac Roberdeau were sent in 1816 with a recommendation from Lafayette. Their mission was to create a corps of engineers for the industrialization of the United States. Claude Crozet developed a corps of engineers at West Point. One of the best students in the class of 1825, Alexander Dallas Bache (the great-grandson of Benjamin Franklin), was sent to Europe to study under Wilhelm Weber and Carl Friedrich Gauss at Göttingen University. Bache would later design the engine boilers for the safest locomotives in the world.
It was West Point engineers like Bache, Stephen Long, and George Washington Whistler, who developed the Baltimore Railroad in the 1830’s. Whistler was also sent to Russia, to build the first railroad from St. Petersburg to Moscow in 1843. The Frenchman Isaac Roberdeau would build all of the fortifications on the East Coast, including Fort McHenry in Baltimore. Roberdeau’s prize work, Fortress Monroe (1830) in Norfolk, Va., made him famous as the “Vauban of the New World.”
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.
 Abrecht Dürer, A Man Drawing a Line, 1525
Abrecht Dürer, A Man Drawing a Line, 1525