
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What’s New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
|
Symposium: THE CREATIVE PRINCIPLE IN ART AND SCIENCESS |

Leonardo Da Vinci, “The Arno”
What Mathematics Can Learn From Classical Music
For related articles, scroll down or click here.
|
Symposium:
THE CREATIVE PRINCIPLE IN ART AND SCIENCE |
What Mathematics Can Learn
from Classical Music
by Bruce Director
‘Heard melodies are sweet, but those unheard are sweeter.’
—John Keats
That the creation and re-creation of great Classical musical compositions is a source of human happiness, is undeniable. Yet, such happiness cannot be relegated to the domain of pleasurable distractions. In fact, it is in the domain of great Classical musical composition, that human beings can and do discover fundamental principles of human knowledge and of the physical universe itself.
As will be shown below, by way of examples and otherwise, the source of human happiness associated with creating, performing, and listening to great Classical musical compositions, arises solely from the mental process of creative discovery associated with such compositions. Consequently, a rigorous examination of the principles of creative discovery, embodied in Classical musical composition, has profound implications far beyond the domain of art. Fundamental issues confronting mathematics and physical sciences are dealt with in the realm of musical composition.
Much effort has been made by the Venetian-led enemies of human knowledge to obscure, degrade, and destroy the science of musical composition. On the one side, the so-called Romantics and modernists have degraded music to the level of pure sensuality, where musical development is lowered to a Benthamite “pleasure/pain” principle. Such evil efforts reduce music to mere alternating erotic episodes of dissonance (pain: tension) and consonance (pleasure: release). On the other side, attempts have been made to sterilize music into an axiomatic array of fixed rules and laws. Unfortunately, most performers and audiences today suffer the effects of these deliberate forms of debasement.
Friedrich Schiller, in “The Aesthetical Lectures,” defines this issue in terms of aesthetics:
The perfect, presented with freedom is immediately transformed into the beautiful. It is, however, presented with freedom, when the nature of the thing appears harmonizing with its technique, when it looks as if it were flowing forth voluntarily from the thing itself. One can also briefly express the preceding so: An object is perfect, when everything manifold in it accords with the unity of its concept; it is beautiful, when its perfection appears as nature. The beauty increases, when the perfection becomes more complex and the nature suffers nothing thereby; for the task of freedom becomes more difficult with the increasing number of compounds and its fortunate resolution therefore, even more astonishing.
All Classical musical composition is inherently paradoxical. The beauty of a musical composition increases with the ability of the composer to maintain a unity of effect throughout the composition, while increasing the complexity (density of change) in the composition. However, it is impossible to state explicitly the unifying idea of the composition; it exists only in the mind of the composer, and subsequently, in the minds of the listeners, as what Lyndon LaRouche has defined as a “thought-object.” This “thought-object” is as real as the notes that are performed and heard, but it cannot itself be heard in the audible domain.
This thought-object is communicated as a properly performed musical composition that is unfolded by the performers over a finite period of time, from the opening notes to the final cadence. As the piece unfolds, the listener is led on a journey of discovery. At the very moment after the final cadence, the entire composition is enfolded in the mind of the listener and grasped as a virtually simultaneous whole. That unifying enfolding occurs only in the sovereign mind of the listener. It is an irreducible One, yet it can come into existence only in the mind of the listener, as a result of the unfolding of the composition over time. The composition exists in time, yet its central idea exists in virtually no time. It unfolds through audible tones, yet its subject, that from which it is generated, is inaudible.
The power of a musical composition is associated with the ability of the composer to create increases in beauty for the listener, as identified above by Schiller. But such increases in beauty are not achieved by simply making compositions more complex. Any increased complexity—a Many—must result only from the creation, first, of a higher conception—a One—from which the complexity is unfolded. Paradoxically, this process is heard by the mind in reverse: the complexity of the composition is what is heard; the higher conception, the One, arises in the mind of the listener, but is unheard.
Such increases in power can themselves be ordered according to what Georg Cantor defined in mathematical terms as cardinalities. Each higher cardinality is characterized by a unity (One), of increasing complexity (Many). Each higher cardinality subsumes all lower ones. Each successive higher cardinality is generated as a solution to a fundamental paradox existing in its predecessor. Such paradoxes are perceived by our senses, in this case hearing, as mathematical discontinuities or singularities. As we will see, the generation of rising powers (cardinalities) of creative thought, is the subject matter of great Classical musical composition.
The Physical Principles of Well-Tempered Polyphony
Before turning to the musical examples, let us first examine some of the physical properties of the audible tones of the well-tempered system of polyphony which externally bound all musical compositions.
The seven octaves—each divided into twelve tones—of the Classical well-tempered system of polyphony, are physically determined singularities of physical space-time. Contrary to the fraud perpetrated by Hermann Helmholtz, which sadly is generally accepted by most musicians and physicists today, these tones are not arbitrary values chosen merely by whim. Each tone is a force-free region of physical space-time, whose value (frequency), like Kepler’s values for the orbits of the planets in the Solar System, is determined by the characteristic properties of a quantized field underlying physical space-time.
The specific frequencies of these tones, centered on middle C = 256 Hz, are revealed by discovering the bio-physical properties of the bel canto qualities of the human singing voice. These discoveries show that there are six separate species of the human singing voice: soprano, alto (mezzo-soprano), contralto, tenor, baritone, bass. Each species has a characteristic set of physiologically determined regions where the singer, in order to maintain a beautiful tone, must shift from one register to another. For example, when C = 256, the soprano and tenor must shift from their middle to high register between F and F♯ [Figure 1].
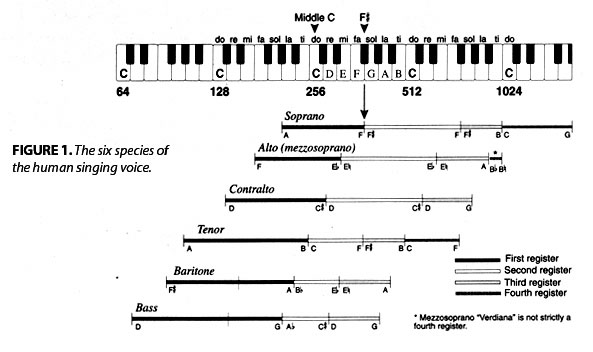
When two or more voices, either a capella or in combination with musical instruments, sing together, it is quickly discovered that a system of tuning is required which is not determined by ratios of whole numbers. Such a non-linear system of tuning is known as the well-tempered system, and was most thoroughly elaborated by J.S. Bach.
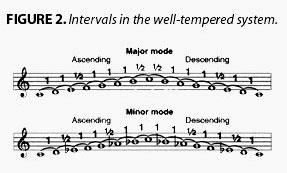
The totality of intervals in the well-tempered system of polyphony can be bound together conceptually, by a unifying ordering principle (order type). The most generalized order type, is associated with the major/minor mode. This order type, elaborated by J.S. Bach, is identified with the twenty-four key, well-tempered system (or, forty-eight key, if ascending and descending are considered, as they should, to be different species) [Figure 2].
Consequently, discoveries in the musical domain are valid discoveries of objective physical principles, as well as subjective ones.
The audible tones of the well-tempered system are externally bounded by a quantized field which is itself “unheard”; yet its properties are nonetheless discoverable through the audible realm. In the workshop of musical composition, the bounding characteristics of this unheard quantized field are revealed by the behavior of the singularities that emerge as musical paradoxes. This property enables the composer to focus the mind of the listener not on the notes, but on change.
For example, the listener never hears a single tone in a musical composition. The listener always hears the interval between tones, that is, the change between tones. And yet, in the well-tempered system, an interval between two notes does not express just one type of change.
Look at the interval of a fifth in the key of C major/minor, i.e., C-G, shown in Figure 2. Ascending from C-G, the listener hears an ascending fifth. This simple interval divides the octave into two distinct intervals: a fifth (C-G) and a fourth (G-C). Going in the reverse direction, i.e., descending from C, generates the interval C-F, i.e., a perfect fifth. An ascending fourth, C-F, is different from its reverse, descending from F to C, because F to C implies the descending fifth.
In addition, any particular interval is changed in relation to specific keys. For example, in the key of C, the fifth C-G, is the interval between the first and the fifth notes of the scale. In the key of F, this same fifth, C-G, is the interval between the fifth and the ninth (second). In the key of G this same fifth, is the interval between the fourth and the octave. In the key of D, this fifth is the interval between the fourth and the diminished seventh.
Therefore, a seemingly simple interval is not really so simple after all. Similar ambiguities exist for other divisions of the octave [Figure 3].
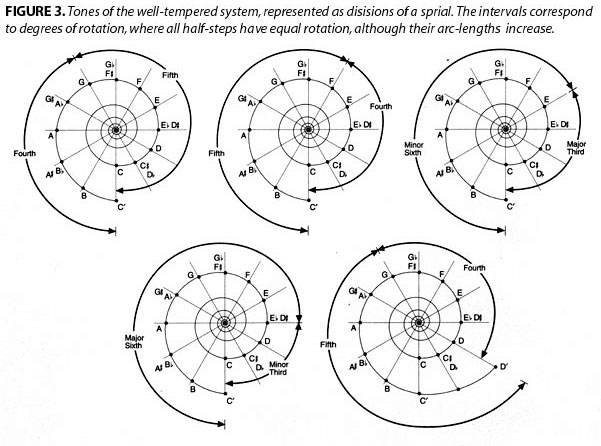
In the major/minor mode, sequences of intervals can be re-ordered, or inverted, according to a specific principle. For example, the first five notes of the major mode can be inverted, thus generating the minor mode, and vice versa. The major mode can be inverted at the octave to generate a minor mode of a different key [Figure 4].

A singularity of significant importance is the interval which divides the octave exactly in half, misnamed the “devil’s” interval or tritone, which were better called the “Lydian” interval for reasons which will become clear later in this report [Figure 5].
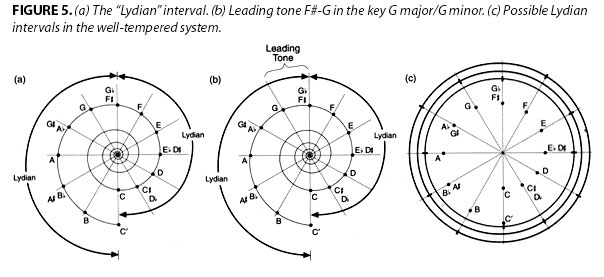
The Lydian interval is the only interval which cannot be generated by the principle of inversion of complementary intervals within any given key. This interval uniquely divides the octave exactly in half: that is, the interval from the tonic to the Lydian tone is the same amount of change as the interval from the Lydian tone to the octave. In the key of C major/minor, for example, this corresponds to the interval between C and F♯, which also corresponds to the physical singularity of the register breaks in the soprano and tenor singing voice [Figure 5(a)]. (above)
Divide an octave in half. This generates a Lydian interval. In the major/minor mode, the Lydian interval is a dissonance with respect to any given key. For example, in the key of C major/minor, the interval C-F♯ is such a dissonance. Yet this Lydian interval has the unique property of being a pathway from one key to the next, by way of the leading tone of that next key (F♯-G in the key of G major/G minor) [Figure 5(b)]. It is a type of singularity to be resolved through the development of the composition.
When the octave is divided in half again, two Lydian intervals are created. There are only three such combinations possible in the well-tempered system [Figure 5(c)]. (above)
An analogy can be made with Cardinal Nicolaus of Cusa’s treatment of the transcendental nature of &Mac185;. When a circle is divided in half by circular action, a diameter is generated, the ratio of whose length to the circumference of the circle, is &Mac185;. Cusa showed that while the value of &Mac185; can be calculated to any decimal value, its exact value is not determinable, because the diameter, a straight line, is of a different species than the circle. When two such different species are compared, a mathematical discontinuity, or singularity, results.
Simlarly, when an octave is divided in half, the Lydian interval, a singularity, is generated which is transcendental with respect to that octave.
Make a partial list of the audible singularities of the well-tempered system of polyphony:
Inversions
Ascending/Descending Intervals
Complementarity of Intervals
Lydian Intervals
Vocal Registration/Instrumental Registration
Now step back and think of a given key, for example, C major, as a unity. See the singularities. Now think of C major along with C minor, and think of these singularities anew. Now think of all twenty-four keys as a whole. Now think of all twenty-four keys as ascending and descending, i.e., all forty-eight keys. With each new mental act, the mind generates a succession of order types.
But the fun is just beginning. What has been described above is simply the natural beauty of the well-tempered system of polyphony, presented to us by God and discovered by that which makes us in the image of God, creativity. Now we must turn to the great scientific geniuses of musical composition, who continue God’s creation with works of artistic beauty.
We will illustrate the principles outlined above with examples from four string quartets. For the purposes of our illustration, we will examine here only the generative principles out of which each of these compositions develops, for the potential development of each composition is contained entirely in the generative idea which creates bounding conditions on it. It is the composer’s genius to discover and reveal this potential. As the composition unfolds, the singularities embedded within the generative principle are subjected to transformations by the composer, and the listener hears development in the composition in terms of the change associated with these transformations. By comparing the generative material from compositions of three composers encompassing the span of approximately forty years, it is possible to see the successive breakthroughs in human conceptual power associated with these creative discoveries.
The string quartet [two violins, viola, and violoncello (’cello)] virtually came into existence through the work of Franz Joseph Haydn. This medium allows for maximum musical transparency, because of the registral characteristics of these stringed instruments when made to sing by performers familiar with the principles of bel canto singing. This ensemble of four voices actually composes a fifth voice, that of the quartet as a whole. The string quartet serves both as the core of the entire symphony orchestra and as a test bed for compositional innovation.
These illustrations, while necessarily partial, nevertheless should serve as a sufficient guide to the reader, to whom we leave the task of exploring, with the ears and the mind, the full richness of these compositions.
Haydn’s Opus 33, No. 3
Franz Joseph Haydn’s Opus 33, the collection of six string quartets composed in 1781, represented a major breakthrough in human knowledge, with the development of a new principle of musical composition called Motivführung, or motivic development.
Here Haydn takes an extremely simple idea and subjects it to transformations across the musical space. The effect is to enable the listener to hear a greater density of change, while maintaining a unity of effect.
Look at the opening seventeen measures of the first movement of Op. 33, No. 3 in C major, the “Bird.” In measure 1, the viola plays repeated eighth-note E’s with the second violin playing repeated eighth-note C’s above [Figure 6].

This interval divides the octave into a major third and a minor sixth. In measure 2, the first violin enters on a G above as a whole note, adding the additional interval of the perfect fifth, and implicitly the minor third and major sixth. In measure 3, the first violin adds a little grace note F♯ to its G, introducing the interval which divides the octave exactly in half. Also, the first violin now divides the measure rhythmically in half. As we identified above, this interval (C-F♯) is at the boundary with the adjacent key of G, and is dissonant with respect to C. Finally, on the first beat of measure 4, the first violin extends the grace note from a half-step below the G, to a whole-step above.
So, in the first three measures, Haydn has, with the simplest means, presented the listener with the primary divisions of the octave in a condensed idea (the fifth, fourth, major third, minor third, major sixth, minor sixth, half-step, and whole-step).
In measures 4, 5, and 6, these divisions are simply unfolded. The ’cello plays the C-E-G of the viola, second violin, and first violin, as an ascending arpeggio. The first violin plays a descending flourish with the F♯ changed back to F natural, thus underscoring the paradoxical character of the initial F♯ grace note. The rest at the end of measure 6 gives the listener a chance to now hear, in his mind, the first six measures as a One.
In measures 7-12, the quartet projects the same motivic idea to a different place, which changes the intervallic relationship between the instruments and generates a new array of singularities [Figure 7].

The viola is displaced up a half-step, from E to F; the second violin is displaced up a whole-step, from C to D; and the first violin is displaced up a whole-step, from G to A. Now the interval between the viola and the second violin is a minor third/major sixth, the complement of the major third/minor sixth of the first measure. The grace note now becomes a G♯, thus preserving the Lydian interval with the second violin. As these next six measures unfold, a new unity is generated in the mind of listener, which is different from the One associated with the first six measures, but, because it is generated out of the first One, the mind easily unifies both ideas into a new One which is associated with the change between the two sections. The mind abstracts from this change that which is universal, but unheard. The rest at the end of measure 12 directs the mind of the listener toward this objective.
In measures 13-17, a still newer transformation is generated out of the previous twelve measures, which, when reflected in the mind of the listener, generates again a new One, causing the mind to abstract again a new universal from this new degree of change [Figure 8].

As they unfold in time, each transformation is discontinuous from the one preceding, yet thinking back, one “hears” the transformations as a continuous process of change.
Haydn places no rest at the end of measure 17, and from measure 18 onward this process continues, unfolding the implications of the initial idea, while the mind enfolds these developments into an “unheard” One, whose beauty increases as “the perfection becomes more complex and the nature suffers nothing thereby.”
In measures 66-73, the density of change is greatest as the implications of the initial motivic ideas are now themselves the subject of development [Figure 9].

The movement ends with the restatement of the initial idea, but this time it is heard in an entirely different way.
Mozart’s String Quartet K. 464
In response to Haydn’s Opus 33, Mozart, over the next few years, composed six string quartets which integrated Haydn’s development of the Motivführung, with J.S. Bach’s discovery and elaboration of the properties of the major/minor mode. Mozart dedicated these six quartets to Haydn. Of particular interest is the string quartet K. 464 in A major, for it is known that Beethoven studied this quartet closely.
Here Mozart increases the density of change by generating the composition from a more condensed motivic idea [Figure 10]. Notice the way Mozart constructs the initial idea such that a seemingly simple, two-measure idea has embedded within it a fundamental paradox. In measure 1, the quartet begins with a simultaneous division of the octave into a major third and a perfect fifth (A-A-C♯-E). In the last half of the second beat of measure 1, the first violin descends one half-step to a D♯, while the other instruments hold their original notes. The listener is presented with the singularity of the Lydian interval when he hears this half-step change from E to D♯ in relation to the A’s of the ’cello and viola. Now the violin, playing alone, ascends up a minor third to F♯, taking it across the soprano’s register shift between F and F♯. Then it descends step-wise a fourth to C♯ (playing a D natural in contrast to the previous D♯). Then it ascends again a minor third to the E on which it started, and then it descends step-wise a fifth to an A, where it is joined by the other instruments which, when combined, play the same notes as those on which the piece began, except, significantly, in a different order (C♯-E-E-A). This time the E is doubled instead of the A.
From measure 3 to measure 4, all four instruments play simultaneous quarter notes. The ’cello descends step-wise a fourth (C♯-B-A-G♯); the viola ascends step-wise a fifth, to B (E-G♯-A-B); the second violin, starting from the same note (E) as the viola, reverses the viola’s direction, and descends to the B an octave lower than the viola, a step-wise fourth (E-D-C♯-B). To summarize, both the viola and the second violin start on the same note (E) and end on the same note (B), but an octave apart. Thus, the second violin ascends a fifth, while the viola descends the complement, a fourth. The first violin then ascends step-wise a fourth (A-B-C♯-D). In addition, the second violin also plays the same E with each note. Even though this E doesn't change its pitch, it is heard differently every time it is played, because everything around it changes.
A new Lydian interval, G♯-D, is formed on the second beat of measure 3, between the viola and second violin, and on the first beat of measure 4, between the ’cello and the first violin.
All instruments rest on the second beat of measure 4, directing the listener to bind what has just been heard, into a One.
Look at the types and density of audible singularities which are presented in these first four measures. For example, the Lydian interval in measure 1; the changes in registration in measures 1 and 2; the difference between ascending and descending intervals, and the complementarity of the fourth and the fifth, in measures 3 and 4. All these singularities are embedded in what Mozart has organized into a seemingly simple idea, which the listener then re-creates in his mind as a thought-object which itself is “unheard.”
From the last beat of measure 4 to the first beat of measure 7, the quartet subjects what has just been heard to a transformation which produces a significant difference in the behavior of the singularities previously generated.
The statement opens with the intervals generated in measure 3 (E-G♯-B-D) which contain the Lydian interval (G♯-D) formed in measures 3 and 4. The first violin then plays the same intervals in measures 5 and 6 as it did in measures 1 and 2, but displaced down one step, starting on D instead of E. This displacement changes the behavior of the singularities thus produced. The violin plays: descending half-step (D-C♯), ascending minor third (C♯-E), step-wise descending fourth (E-B), ascending minor third (B-D), step-wise descending Lydian (D-G♯) (instead of descending step-wise fifth, as in measure 2). In opposition to the opening, the new Lydian interval is this time heard in the notes played by the whole quartet at the beginning of the statement, but it disappears when the first violin plays alone.
Note the generative quality of the half-step interval D-C♯-D-C♯ in the first violin in measures 5 and 6, in contradistinction to the generative quality of the intervals E-D♯-E-D-natural in measures 1 and 2.
Measures 7 and 8 imitate measures 3 and 4, but again with significant differences. The first violin ascends step-wise a fourth, as in measure 3, but this time starting a half-step lower (G♯-A-B-C♯). (Of course, this changes the internal relationships between the steps from whole-step, whole-step, half-step, in measure 3, to half-step, whole-step, whole-step here.) The second violin ascends step-wise a fourth (E-F♯-G-A), in contrast to the step-wise descending fourth from the same note in measure 3. The ’cello takes the E from the second violin in measure 3, but plays this note as one continuous tone, instead of four separate ones, and then descends a fifth to A. The viola descends a minor third by half-steps (E-D♯-D-C♯). Notice the formation of the two previously heard Lydian intervals, D♯-A on beat two, and, D-G♯ on beat three.
The second beat of measure 8 is a rest, to allow the listener to form what has just been heard into a new thought-object. As we have seen, measures 5-8, being a transformation of measures 1-4, seem to imitate them, but with significant differences. Those differences are heard as changes in the behavior of the audible singularities presented. Now the listener forms in his mind an abstraction of what is the same, and what has changed, between these two thought-objects, a new One which, while “unheard,” is as real as the audible tones from which it was generated.
From the last beat of measure 8 to the first beat of measure 12, all four instruments play the same notes (with the ’cello playing an octave lower). Such a unison focuses the listener intensely on this more condensed form of what has been heard in the previous measures. In measure 9, the quartet ascends a major third (A-C♯) taken from the very first notes of the piece; then ascends and descends the half-step C♯-D (the generative interval of measures 5 and 6); and then descends a whole-step, to end on a B. In measure 10, after a rest, the quartet, drawing on the generative interval of measures 1 and 2, starts on that B, and again ascends a major third (B-D♯), ascends again a half-step (D♯-E), but then descends a whole step to D-natural, and then descends a half-step to C♯.
This is a condensed and more generalized restatement of the singularities embedded in the first nine measures; yet, such a restatement would have been impossible without what has been previously unfolded.
After another rest, the quartet plays the opening notes (C♯-E-A-A) in different registers, and in measure 13, the first violin ascends the major third (A-C♯), then descends step-wise an octave and a fourth, as the quartet completes the initial development on the same notes—an octave lower—on which it began (A-A-C♯-E) (measure 16).
Think back on what has been unfolded over these opening sixteen measures. The piece began with a seemingly simple statement, rich in singularities. This statement was then subjected to a transformation, presenting to the listener—paradoxically—change and no change. Then, the generative principle of the transformation was abstracted out, and put in contradistinction to the generative principle of the original statement. Finally, everything was brought together in a concluding statement. Nothing was arbitrary. Every development arose out of the opening idea which Mozart had so skillfully chosen.
Each step required new powers of thought for the listener. The listener’s happiness increases as he discovers the ease with which the powers of his own mind rise, seemingly effortlessly, on the beautiful tones of Mozart’s composition.
And this is only the first sixteen measures! The reader is encouraged to compare the kind of change represented here, with what was examined previously in the Haydn example. Space limitations prevent us from fully exploring this composition. We will, however, indicate several places for the reader to explore on his own.
Look at the last beat of measure 16. Here Mozart changes the C♯ to a C-natural, bringing us into the minor mode. The opening idea is now subjected to even more rapid transformations in measures 16-24. Here, Mozart achieves a density of change which is not achieved in the Haydn example until measure 66. [Figure 10, measures 16-24].

In addition to the increased density of change in this Mozart example, there is a unity across the movements, extending the Motivführung principle to the entire composition. For example, the entire last movement, is generated from the three descending half-steps E-D♯-D-C♯ (minor third) in measures 1-2, stated by the viola in measure 7 of the first movement, embodying the initial paradox stated in the first movement, but now heard by the listener in an entirely different way [Figure 11].

Beethoven’s Opus 59, No. 2
After extensive study and development of all previous music, Beethoven extended human knowledge further, reaching the greatest compositional power in his late string quartets. To more adequately grasp the significance of those developments, let us first stop along the way and see the formation of his later ideas in their earlier stages.
In 1806, Beethoven composed three string quartets dedicated to the Russian Count Razumovsky, published under Opus 59. In these quartets, Beethoven explored the boundary conditions of the major/minor mode, embarking on a course which ultimately led to his discovery of a higher ordering principle of musical space, elaborated in the late quartets. A look at Op. 59, No. 2 in E minor illustrates the point.
The first movement opens with two chords played by all four instruments of the quartet (E-B-E-G-B-E-E minor; D♯-B-E-B-F♯-B-B major) marked forte and separated by an eighth-note rest [Figure 12].

These two chords present the listener, implicitly, with the boundary conditions of the major/minor mode. The full measure rest [measure 2] directs the listener to form in his mind a unified conception of these conditions.
In measures 3 and 4, measure 1 is unfolded by the first violin and ’cello playing in octaves, a descending fourth, E-B, ascending minor sixth, B-G, and ascending major third, G-B. The first violin continues, ascending to C, and then playing three rapidly descending minor thirds (C-A-F♯-D♯), a descending major third (D♯-B), and an ascending fourth (B-E: the inverse of the first interval of measure 3). Embedded within this descending violin line are two Lydian intervals (C-F♯, A-D♯: the octave divided in half twice). The full measure rest that follows [measure 5] directs the listener to enfold into a One what has just been unfolded.
In measures 6 and 7, joined now by the viola, this same idea is projected up a half-step to F, with the ’cello dropping into a lower register. This projection changes the complementary intervallic relationships of measure 3: descending fourth (F-C), ascending major sixth (C-A), ascending minor third (A-C). The order of the intervals in the descending violin line in measure 7 is changed to, first, a descending major third (D-B♭), followed by two descending minor thirds (B♭-G-E), a descending major third (E-C), and an ascending fourth (C-F). Notice the invariance of the fourth while the other intervals change.
The full measure rest that follows [measure 8] now directs the listener to hear—as a One—what this projection has changed, and not changed, and to abstract in the mind that which is universal about this development.
In measure 9, Beethoven presses the boundaries of the major/minor mode. The viola begins alone on F♯, up another half-step from the previous section, but instead of descending a fourth as in measures 3 and 6, the viola descends a minor third, as in the violin line of measures 4 and 7, bringing it to the D♯ of the ’cello in measure 1. Then, instead of ascending a major or minor sixth, the viola ascends a Lydian interval to A. Because the viola keeps the same rhythmical pattern as in measures 3 and 4, the listener hears this intervallic change in relation to those measures. The line continues, jumping now to the first violin, which in a new register begins on D♯ as the viola holds its A. Thus, the listener hears the unique halving of the octave by the Lydian interval (D♯-A-D♯). Following the viola, the first violin descends a minor third (D♯-C), and then ascends a Lydian interval to F♯. So the sequence just heard is F♯-D♯-A-D♯-C-F♯ .
Instead of the full measure rest that followed every previous statement, the quartet now “rests” for the first half of measure 10 on the seemingly unstable Lydian intervals now played together (D♯-A-C-F♯). In the second half of measure 10, the first violin descends a half-step to B-natural, resolving one of the Lydian intervals into a fifth (B-F♯). This new type of “rest” directs the listener to form a new type of One.
In measure 11, the first violin begins where it last ended on F♯, and plays, an octave higher, the viola part from measure nine (F♯-D♯-A). The second violin plays different intervals starting on D♯, descending a major third to B, and ascending a fifth to F♯. This is followed by the ’cello, which preserves the intervallic relationships of the first violin, but starting on A, descending a minor third to F♯, then ascending a Lydian to C. In measure 12, the quartet “rests” again, on the same notes as in measure 10, but in a different order (C-D♯-F♯-A).
Taking advantage of the leisure afforded us by our written medium, let us summarize what has just been unfolded. In measure 1, the quartet presented us with the minor mode, and after a rest, we were presented with the major mode. We were given a full measure rest, to form in our minds something that had not been stated in this combination, the thought-object of the major/minor mode. Then this was unfolded, first from E in measures 3 and 4, then a half-step higher in measures 6 and 7. Each time, new singularities—implicit in measure 1—were revealed. This change caused us to form a new thought-object in our minds. The Lydian intervals embedded in measures 4 and 7, were then unfolded in measures 9 through 12, which change caused us to form yet again a new thought-object. This process continues throughout the movement. For example, in measure 19, the Lydian intervals arrived at in measure 10, are now stated as the opening chords of measure 1, but which now are themselves unfolded in yet another new way which is itself not possible without the development that preceeds it.
The reader should now compare this opening with the Haydn and Mozart examples. See the greater complexity (density of change), while the unity of effect is not lessened, indicating to us a higher “unheard” idea.
To get a sense of what potential has been developed in this opening, let’s look briefly at the second movement, marked, “Molto Adagio. This piece is to be treated with much sentiment,” which presents a further development—but in an entirely different mood—from the first movement, where the unfolding proceeds more slowly and contemplatively [Figure 13].

This movement has two parts, which, combined, form an “unheard” third idea. As we will see, Beethoven will turn back to this form in his late quartet, Op. 132.
In the first seven measures, the quartet functions as a four voice “chorus,” presenting various singularities of the major/minor mode. This is followed by an unfolding. In measures 52-56, this “chorus” returns, followed by a new unfolding. In measures 138-143, this “chorus” returns again, followed by a final unfolding. Each time the chorus returns, the unfolding which follows is changed.
In measure 1, the first violin begins with a descending half-step (E-D♯), extracted from the ’cello in measure 1 of the first movement. Each voice enters, in the low register, a fourth below and two beats after the previous entrance. This is heard in reference to measures 3 and 6 of the first movement. The ’cello enters on C♯ and, like the first violin, descends a half-step to C-natural; this leads in measure 3 to the Lydian intervals (C-F♯-D♯-A), which are again heard in reference to the first movement’s development.
In measure 4, the second violin descends two half-steps (E-D♯-D-natural). When the D-natural is heard, the rest of the quartet stops. Instead of a complete rest, as in the first movement, to allow for the formation of a One, here the listener hears both the D-natural and the “unheard” rests. When the first violin re-enters in measure 5 on a B, played now in the middle register, this combination of the heard and the “unheard,” creates an ambiguity which allows the listener to “hear” the major and minor as one unified mode. This is the inverse of the opening of the first movement (E minor/B major in the first movement; E major/B minor here.)
On the first beat of measure 7, the “chorus” presents the listener with a new Lydian interval (E-A♯), which forms the boundary with the next key, B major. This interval is played forte (loud) for emphasis, and in contrast to the piano (soft) played both before and after it.
What follows is a beautiful unfolding beginning on B, which is best heard directly by the reader. In measures 43-47, the first violin counterposes this transition to B with all twelve tones of the well- tempered system [Figure 14].

In measures 52-56, the “chorus” returns, this time in a higher register [Figure 15].

When the unfolding resumes, the A♯ has changed back to an A. In measure 123-126, the first violin counterposes the notes of E major to all twelve tones of the well-tempered system [Figure 16].

In measures 138-143, the “chorus” returns a final time, followed again by the unfolding [Figure 17].

Each chorus presents a variation of the opening seven measures, but each is heard in relationship to the previous unfolding. This juxtaposition of such seemingly different ideas, generates a new thought-object in the mind of the listener.
Beethoven’s Opus 132
Approximately twenty years after composing the Razumovsky quartets, in what were to be the last years of his life, Beethoven composed a series of five string quartets and “Grosse Fuge,” which comprise the highest development of musical science achieved to this day. In these quartets, Beethoven launched a revolution in musical composition, by elaborating a new ordering principle for the well-tempered system, which corresponds to a higher power of thought. The singularities of the major/minor mode are seen in an entirely new way; the boundaries between keys are dissolved and the entire well-tempered system is conceptualized under a new more generalized order type. In mathematical terms, this new ordering principle externally bounds the major/minor mode of the well-tempered system.
At a future time we will examine more fully all these revolutionary compositions. For now, let’s look at Opus 132 in A minor, which includes the famous third movement marked, “Heiliger Dankgesang eines Genesenen an die Gottheit, in der lydischen Tonart” (“A holy song of thanks to the Divinity, in the Lydian mode”).
The Lydian mode is a division of the octave based on the F-major scale with a B-natural instead of the B♪. This ordering has the unique property, that the interval which divides the octave in half, identified as the “Lydian” interval above, is part of the mode itself, i.e., F-B-natural. However, the potential for compositional freedom is less than in the major/minor mode, because the Lydian mode lacks the major/minor mode’s complementary relationship between the fourth and the fifth [Figure 18].
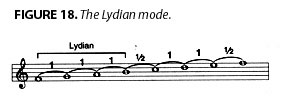
Ironically, Beethoven generates, by reference to this combination of the Lydian mode and the major/minor mode, a higher modality, subsuming the properties of both.
This higher modality or ordering principle of the well-tempered system, is neither the Lydian mode, nor the major/minor mode, nor a simple summation of the two. The higher ordering principle corresponds to a higher power of conceptualization, which Beethoven elaborates through the composition of these last quartets. The listener hears the results of this creative process in the greater density of change achieved in the compositions. At all times, however, Beethoven maintains a unity of effect, because he adheres rigorously to all the principles of Classical musical composition established by the creative discoveries of his predecessors.
After Beethoven’s death, the so-called Romantics and moderns made every effort to destroy Beethoven’s accomplishment, by claiming that Beethoven, in the late quartets, had liberated them from the constraints of Classical tonality. They were enamored with the greater potential for sensual effects resulting from this perceived “liberation.” Not surprisingly, what they produced is best described as organized, or in some cases disorganized, noise.
Beethoven’s new conception is expressed in the opening eight measures of Opus 132. Here, the quartet imitates a four-part chorus of human singing voices, announcing the new idea in song [Figure 19].

The piece begins with the ’cello playing—alone, in a low register, and very softly—the ascending half-step G♯-A. Each tone of this interval is equal in time and volume, creating an ambiguity because the listener cannot tell which one is primary. This interval references what a physicist would call a boundary condition. The G♯ is the leading tone to the tonic A, and at the same time the Lydian interval to D.
But there is a further ambiguity. Is this interval that of the leading tone to the tonic, or is it that of the fifth to the minor sixth of C minor, or that of the third to the fourth of E, etc.? Or is it many things at once?
In measure 2, the viola, in its low register, reverses this interval at an octave higher (A-G♯), which reinforces the ambiguous nature of the opening interval. At the same time, the ’cello, in a different register, also plays a descending half-step, but on different tones (F-E). This also references a boundary condition: the minor sixth to the fifth, and the tonic to the leading tone in F.
Aided by the transparency provided by the change in registration the mind of the listener goes two places simultaneously: G♯-A-A-G♯ (’cello to viola); and G♯-A-F-E (’cello).
While the mind is forming an “unheard” idea from the comparison of these two heard intervals, the second violin enters, on the last two beats of measure 2, on a B in its low register.
In measure 3, the first violin, in its low register, projects the opening interval up a fifth, playing the ascending interval D♯-E. This also references a boundary condition, as D♯ is the Lydian interval to the tonic A, and the leading tone to E. Simultaneously, the second violin plays exactly the same tones as the viola in measure 2, the descending half-step A-G♯; but, significantly for purposes of transparency, the difference in tone between the viola and the violin causes this to sound different. The viola, at the same time, projects the ’cello’s F-E up a fifth, playing another descending half-step (C-B), which references a different but similar boundary condition.
Measure 4 continues the projections just begun. The first violin continues the projection up a fifth from the ’cello line, changing registers and playing the descending interval C-B an octave higher than what was just played by the viola. In imitation, the viola plays what the first violin just played, but drops an octave instead. The first violin returns to the low A, adding an F♯ and a G♯.
Before going on, let us look at what has been generated in these first four measures. By simple projection, inversion, and registration of the opening ascending half-step, Beethoven has juxtaposed a multitude of boundary conditions for the listener, which enable him to form in his mind an “unheard” conception of the manifold from which these boundary conditions arise. Evidencing these boundary conditions are the Lydian intervals (A-D♯) produced between the two violins in measure 3, and the Lydian intervals generated in measure 4 (A-D♯ between the viola and second violin, and F♯-C between the two violins).
The ’cello re-enters in measure 5, repeating measure 2 (F-E). The viola jumps to a high register and inverts the first violin line from the previous measure 4, playing the ascending interval B-C. The second violin, still in a low register, plays the descending whole-step D-C, and the first violin jumps to a higher register and repeats its first two notes (G♯-A). Measure 6 continues this process of inversion, projection, and registration. The violin, still in the high register, mimics the viola’s inversion of its own line, playing the ascending half-step B-C. The second violin mimics the ’cello’s F-E, and adds a C. The viola mimics the second violin from the previous measure (D-C), and the ’cello mimics its own opening (G♯-A), which is now heard in an entirely different way from when those same notes were first presented to the listener.
With each new transformation, the listener hears an increasing density of combinations of boundary conditions, as evidenced by the generation of Lydian intervals: in measure five, F-B between the ’cello and viola, and D-G♯ between the violins; and these same intervals in different order in measure 6, G♯-D between the ’cello and viola, and F-B between the two violins.
Further projections and transformations occur in measure 7. The first violin inverts itself (C-B). The second violin inverts the opening ’cello notes (A-G♯). The viola mimics the second violin from measure 4 (F♯-G♯). The ’cello drops to its lowest register, projecting its opening notes (D♯-E) down a fourth,, which were themselves already played by the first violin as a projection up a fifth in measure 3.
Again, new orderings of these boundary conditions are produced, evidenced by the generation of more Lydian intervals: D♯-A between the ’cello and second violin; F♯-C between the viola and first violin.
A new ordering is generated in measure 8, leading to the rapidly descending minor thirds of the first violin in measures 9 and 10.
Reflect again on these amazing eight measures. Because everything in them is generated by projection, inversion, and registration of the ’cello’s ambiguous opening two notes, there is a total unity of effect across all voices and all measures. And, because these two notes themselves reference a boundary condition, while at the same time are ambiguous, there is a greater density of singularities produced. As a result of these two considerations, the mind is led to create a new and higher conception, a reflection of Beethoven’s new ordering principle which is of a higher cardinality.
Compare these first eight measures with the previous examples of Haydn, Mozart, and Beethoven. In those examples, the singularities were embedded in the opening intervals, and revealed as those intervals were unfolded. Here the opening interval is itself the singularity.
Having created a new and higher conception in the mind of the listener, Beethoven now puts the listener to work exploring the implications of this discovery. First, in measure 11, the ’cello condenses the first eight measures into a singing line played in its highest register (A-B-C-B-A-G♯), ending ironically on the leading tone (G♯), the same tone on which the piece began.
These tones have been abstracted from the opening eight measures, in the manner Cantor defines for the generation of transfinite numbers; that is, each tone played by the ’cello in this measure, is heard in relationship to the tonality defined in the first eight measures.
For example, in measures 103-106, the entire quartet restates fortissimo the first violin’s opening line, which itself is a projection from the ’cello’s opening [Figure 20].

In measures 193-202, the opening notes are juxtaposed to the ’cello’s abstraction, forming a new thought-object from the combination of the two [Figure 21].

Now, look at the previously mentioned third movement. This movement is composed of five sections: three are marked Molto Adagio and written in the Lydian mode, alternating with two marked Andante and written in D major [Figure 22].

The movement begins with one of the Molto Adagio sections. Here, the quartet again assumes the role of an imitation human vocal choir, singing, as a canon, this holy hymn of thanks to God. These sections are written solely using the eight tones of the Lydian mode, with no sharps or flats, yet there is no lack of development.
The first violin starts alone, ascending a major sixth (C-A) which crosses from a low to a middle register. The violin then descends a whole step to G, and ascends a fourth to C. At the same time, the second violin enters, repeating the ascending major sixth (C-A), but then descending an octave to G in the low register, and then repeating the first violin’s ascending fourth to bring it back to its original C [measure 1]. The second violin also adds an E, making explicit the minor third implied by the major sixth (C-A). On the last two beats of this measure, the viola enters, in its low register, repeating again the rising major sixth (C-A), and then continues the line in the next measure, dropping to G and ascending to C, as the ’cello enters with the ascending sixth (C-A) [measure 2].
So in these first two-and-a-half measures, the intervals, ascending sixth, descending whole-step, and ascending fourth, are played as a sequence horizontally (over time) as well as vertically (simultaneously), explicitly directing the listener to “hear” the interval between the intervals. Here the audible singularities generated by complementary intervals—ascending in comparison with descending—and registration, are clearly heard.
In measures 6-8, these intervals are projected and inverted. The first violin, in a high register, starts on A, descends a fifth to D, ascends step-wise a fourth to G, descends step-wise a minor third to E, and finally descends a major sixth to G. The second violin follows the first, except the descending fifth (A-D) is in a lower register, and then it descends a fifth to G—contrary to the first violin’s ascending fourth to G. The viola enters with the descending fourth (A-D), but the ’cello introduces something new, a descending minor sixth (G-B) hearkening back to the ascending minor sixth (A-F) of the first movement. This generates the Lydian interval F-B between the ’cello and the first violin, which is generated again two beats later between the viola and second violin.
In measures 12-13, these same intervals are projected in the ’cello, down and into a different register, to G; they are then projected up into a different register in measures 18-19, by the first violin. In measures 24-25, we are back to the opening, but in different registers.
As this section unfolds, the listener seeks to form a One, but because of the ambiguous way the intervals are presented, that One cannot be associated with any particular key or succession of keys. Instead, the listener’s mind must form a One that is “above” the separation between keys. Compare this to the “choral” opening measures of the first movement, which achieve a similar effect, but from a different direction, so to speak.
The thought-object thus defined is a new and higher conception of the ordering of the well-tempered system.
The entire Molto Adagio is brought into a One with the abrupt shift to the Andante at measure 31. Suddenly, the quartet switches to D major, formed by changing the F to F♯ (the Lydian of C) and the C to C♯ (the Lydian of G). Beethoven subtitles this section “Neue Kraft fühlend” (“Feeling new power”), something experienced immediately by the listener.
With the unfolding of this section, the listener forms two distinct objects in the mind: the One associated with the Molto Adagio and the One associated with the following Andante. These now form a new “unheard” One in the mind.
The Molto Adagio returns, but this time changed. The opening intervals are the same (C-A-G-C), but the duration of the G and the second C are cut in half, and are now played as eighth notes, creating a greater density of effect [Figure 23].

This more developed section is again compared in the mind of the listener with the previous two sections, forming yet again a new One.
After thirty-one measures, the Andante returns. This is again followed by the Molto Adagio, this time marked, “Mit innigster Empfindung” (“With more fervent sentiment”) [Figure 24].

Now Beethoven directs the listener to combine everything previously heard, into a newer One. This is achieved by increasing the density yet again, through a rhythmical change and adding a D, which references the Andante section, to the generating intervals (C-A-G-C-D-C). This creates in the mind a combination of the seemingly disparate previous Molto Adagio and Andante sections. This combination reveals an even greater potential implicit in this new and higher conception, lifting the listener to new powers of thought and reaching a peak with the condensation articulated in measures 191-192 [Figure 25].

Beethoven did not limit the new musical conceptions presented in Opus 132 to just one composition, and it were useful, before ending this report, to point the reader to other examples from among the late quartets, so that you may explore them for yourself.
In Opus 131 in C♯ minor (written after the Opus 132, although published earlier), for example, Beethoven opens with a fugue generated from an ascending and descending major third, separated by a half-step. [Figure 26].

These intervals, like the opening to Op. 132, are on the boundaries and generate ambiguities, such as; is the B♯ to C♯ the leading tone to the tonic of C♯ minor or is it the third to the fourth of G♯ minor? From this Beethoven unfolds the longest of his late quartets.
Or, we have the extraordinary “Grosse Fuge,” in which Beethoven composes an entire fugue from a motivic idea made up wholly of singularities generated by the boundary conditions embedded in the well-tempered system [ Figure 27].

Looking Back
Now, look back at the four compositions: Haydn’s Op. 33, No. 3; Mozart’s K. 464; Beethoven’s Op. 59, No. 2; and Beethoven’s Op. 132. Construct in your mind, as a One, the successive increases in conceptual power, won for us by the creative work of over forty years by three of the greatest geniuses humanity has ever produced. From our vantage point, looking back, we can see the kernel of each successive development embedded in the previous one. It appears continuous—but it wasn't. For each successive breakthrough occurred only by a discontinuous leap, secured solely through the creative powers of the composer—the same creative powers which, through these compositions, we may sometimes glimpse in ourselves.
What is the Schiller Institute?
Other Schiller Institute Articles by Bruce Director:
Bernhard Riemann’s ‘Dirichlet’s Principle’
Carl Gauss’s Fundamental Theorem of Algebra
Riemann for Anti-Dummies on the LaRouche Youth Movement Website
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What’s New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2005 All Rights Reserved.
