
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
 |
||||
|
Nicloaus of Cusa
|
||||
On the Quadrature
of the
Circle
1450
Nicolaus of Cusa
For related articles, scroll down or click here.
ON THE QUADRATURE OF THE CIRCLE is one of several written by Nicolaus of Cusa (1401-64) on this subject during the 1450's. The first reference in his writings to this topic appears in ON LEARNED IGNORANCE (1440), where he writes that “a noncircle cannot measure a circle, whose being is something indivisible.”
In many of his writings, including “LaRouche's Discovery” in this issue of Fidelio, Lyndon LaRouche has identified the importance of the method employed and the conclusion attained by Cusanus in this work, as the unique basis for the development of modern science. We publish this translation as an historical source document, the mastery of which is vital to a full appreciation of Lyndon LaRouche's own scientific method.
The translation, which appears below, is not of the original Latin text, but rather of a German translation which appears in DIE MATHEMATISCHEN SCHRIFTEN VON NIKOLAUS VON KUES, published by the Felix Meiner Verlag, Hamburg.
You assert that you are involved with a multitude of commentators on the quadrature of the circle, and you urge me, now, since the needed leisure is provided, to give you an exhaustive presentation of what can be known about this subject. Receive my intuition now in the following proposition. But know, that on your behalf I have so treated the subject, that, after leaving the mathematical sciences, you can proceed more easily, through assimilation of this discussion, to the domain of theology.
Proposition
There are scholars, who allow for the quadrature of the circle. They must necessarily admit, that circumferences can be equal to the perimeters of polygons, since the circle is set equal to the rectangle with the radius of the circle as its smaller and the semi-circumference as its larger side. If the square equal to a circle could thus be transformed into such a rectangle, then one would have the straight line equal to the circular line. Thus one would come to the equality of the perimeters of the circle and of the polygon, as is self-evident.
These people also allow for the following conclusion, without which they could achieve nothing, namely: Where one can give a larger and a smaller, one can also give an equal. Since one can give a square larger than the circle—as is the circumscribed—, and a smaller—as is the inscribed—, therefore there is also an equal, which is neither circumscribed nor inscribed, but rather is in like manner circumscribed and inscribed. They let the same manner of conclusion hold also for the perimetric lines: Since a circumference greater than the perimeter of a triangle can be given—as is the perimeter of the circumscribed circle—, and since a circumference smaller than the perimeter of a triangle can be given—as is the perimeter of the inscribed circle—, a circumference equal to the triangle's perimeter can also be given, and this circle is neither circumscribed nor inscribed, but rather is in like manner circumscribed and inscribed.
There are also scholars, who deny the possibility of the quadrature of the circle, and these dispute all the aforesaid. They assert, namely, that in mathematics the conclusion does not hold: Where one can give a larger and a smaller, there one can also give an equal. There can namely be given an incidental angle that is greater than a rectilinear, and another incidental angle smaller than the rectilinear, and nevertheless, never one equal to the rectilinear. Therefore with incommensurable magnitudes this conclusion does not hold. That is to say, if one could give one incidental angle that is larger than this rectilinear angle by a rational fraction of the rectilinear, and another that is smaller than this rectilinear by a rational fraction of the rectilinear, then one could also give one equal to the rectilinear. But since the incidental angle is not proportional to [commensurate with] the rectilinear, it cannot be larger or smaller by a rational fraction of the rectilinear, thus also never equal. And since between the area of a circle and a rectilinearly enclosed area there can exist no rational proportion—as little as between the incidental and the rectilinear angle—, therefore the conclusion is also here not permissible.
That will be obvious in the following: Every magnitude which can be converted into another, is necessarily such, that each of its parts could also be part of the other magnitude, since the whole is nothing else than the sum of its parts. A segment that is cut off from a circle by a straight line cannot, in respect to its incidental angles, which are parts of its surface, be transformed into a rectilinearly enclosed figure; therefore also not in respect to its totality. But this is palpable: If a circle can be transformed into a square, then it necessarily follows, that its segments can be transformed into rectilinearly enclosed figures. And since the latter is impossible, the former, from which it was deduced, must also be impossible. Obviously, then, the semicircle cannot be transformed into a rectilinearly enclosed figure, and consequently also not the circle or one of its parts.
Every incidental angle exceeds another or is exceeded by it, by the amount of a rectilinear angle, to which it can have no rational proportion. From this it ensues, that all segments of a circle produced by straight lines are in no wise proportional to the circle. And since the largest segment is produced by the diameter, all other segments are not proportional to this. Therefore no rational fraction of the circle can be cut off by such lines, because this fraction is non-proportional to the greatest segment, that is, to the semicircle. Therefore the following proposition does not hold: One can cut off from the circle a segment greater than a third of the circle and another smaller than a third of the circle, and therefore also one equal to a third of the circle. From this it ensues: Segments of a circle, which are produced by a straight line which is smaller than the diameter, can in no way be transformed into rectilinearly enclosed figures because they are rational parts of the circle, but rather because the quadrature of the circle would follow therefrom, if they could be transformed into rectilinearly enclosed figures.
From that you can make clear to yourself, that everything is impossible from which the quadrature of the circle follows. The circle, therefore, because of its uniqueness, has the following property: Just as the incidental angle cannot be transformed into a rectilinear, so the circle cannot be converted into a rectilinearly enclosed figure. However, a rectilinear angle can be given that is larger than the incidental angle by the contingent [horn] angle.—The contingent angle is a divisible magnitude only in its species, since to every contingent angle there is a larger and a smaller contingent angle.—Although the contingent angle is smaller than any rectilinear, nonetheless in this manner one can give a rectilinear angle larger than a given incidental angle, which however is not larger by a rational fraction of the rectilinear angle. Just so, one can give an incidental angle smaller than a given rectilinear angle, and indeed, smaller by the amount of the contingent angle, which is not however a rational fraction of the incidental angle, but rather smaller than any rational fraction of the same.
In the same way one can say: For a given circle a square can be given, which is in fact larger than the circle, however, not by a rational fraction of the square. And for a given square a smaller circle can be given, which is not however smaller by a rational fraction of the circle. From this follows: To a given circle a larger square can be given—larger, however, not by a rational fraction; and to every so given square another can be given that comes nearer to the circle, but none that is precisely equal to it. And none that is smaller than the circle by a rational fraction, likewise vice versa.
And this view I regard as the more correct. Because, since polygonal figures are not magnitudes of the same species as the circular figure, even if a polygon can be found that comes nearer in magnitude than another to a given circle, the proposition nonetheless holds true that: In respect to things which admit of a larger and smaller, one does not come to an absolute maximum in existence and potentiality. Namely in comparison to the polygons, which admit of a larger and smaller, and thereby do not attain to the circle's area, the area of a circle is the absolute maximum, just as numerals do not attain the power of comprehension of unity and multiplicities do not attain the power of the simple.
It seemed to suffice those people, who adhere to the first view, that in respect to a given circle a square can be given that is neither larger nor smaller than the circle. Every larger magnitude is namely larger by a fraction of itself or of another magnitude with which it is compared. It is likewise with the smaller. But if the square that can be given is also not larger or smaller than the circle by the smallest specifiable fraction of the square or of the circle, they call it equal. That is to say, they apprehend the concept of equality such that what exceeds the other or is exceeded by it by no rational—not even the very smallest—fraction is equal to another. If one apprehends the concept of equality in this way, then I believe one can justly say: To a given polygonal perimeter one can give an equal circumference, and vice versa. But if one apprehends the concept of equality, insofar as it relates to a magnitude, absolutely, without regard to rational fractions, then the statement of the latter is correct: No precisely equal non-circular magnitude can be given for a circular magnitude; and this by means of explanation of the thought that underlies the cited proposition: If to a given perimeter of a triangle, etc. So much should suffice. From this you may grasp what you find presented in various ways about this subject in some of my other writings.
Explanation of the Proposition
In order to explain the proposition, a triangle abc shall be drawn (SEE Figure 1); around the midpoint d shall be inscribed a circle efg and a circle hi circumscribed; the straight line de shall be so drawn, that e is the midpoint between a and b; then db shall be drawn. Further, a straight line dk shall be drawn from d to the midpoint between e and b. I maintain: dk is smaller than the radius of the circle isoperimetric to the triangle, by one-fourth of the length dk.
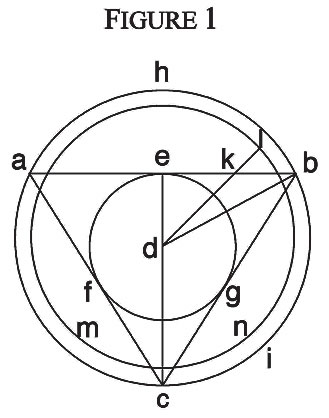 |
||
In order to prove this assertion, I proceed in the following manner: I say, if it is possible, to draw a straight line from d to eb, that is the radius of the circle isoperimetric to the triangle, then it must be to the sum of the sides of the triangle as the radius of the circle is to the circumference. But since the radius has no rational proportion to the circumference, neither as a linear magnitude nor as power, that is, since the square area of the radius, which represents the second power, has no rational proportion to the area of the circle, it also had no rational proportion to the square area of the circumference, if one could give this. Clearly therefore neither the sought line itself nor its square can be proportional to the length de or db, whose squares are proportional to the square of eb. Therefore one cannot draw that line from d such that it stands in rational proportion to eb or db, just as the endpoint k located from e toward b will not be removed from e by a length proportional to eb or db. If this were so, then the square would be always proportional to the square of eb, which is self-evident. Consequently, no point on eb can be given, to which one could draw a line, which were precisely that sought. But there is indeed a point on eb, to which one can draw a line, that is neither larger nor smaller than that sought, and indeed by no rational fraction, as small as it may be. Consequently I maintain: Just as no length, which can be drawn from d toward eb according to an rational point of division of eb, can be the sought length, just so little can such a length standing in rational proportion to eb, be proportional to the sought one, as is self-evident, since the squares of all of these lengths are proportional to the square of eb.
I maintain finally: Even if no such length is precisely proportional to the one sought, nevertheless the one will be more proportional than the other. And this is clear; for even if all were non-proportional to de and eb, nonetheless the one is more proportional to eb and db than the other, and therefore less proportional to the one sought. Hence that one, which is most non-proportional to eb, de and db, is of all the least non-proportional to the one sought. Therefore, one length of all those that can be drawn from d toward the points of division of eb will be less non-proportional to the one sought.
On the Search for Proportionals
But in order to investigate the proportionals, one must pay attention to the following: Among the non-proportional lengths, some are like the side and diagonal in the square, and a proportion so precise can never be found, that the divergence is not larger than a rational fraction. For example, a tenth of the diagonal is smaller than a seventh of the side, and the divergence is larger than a rational fraction of the diagonal and of the side; and likewise in the smallest parts.
Another non-proportionality is that of the incidental and the rectilinear angle, because a length that corresponds to the incidental angle is non-proportional to a length that corresponds to a rectilinear angle, and the half of the rectilinear angle is larger than the half of the incidental angle, and indeed by the half of the contingent angle. This half is however smaller than any rational fraction of the rectilinear as of the incidental angle.
But that such a proportion can be found in lengths, becomes evident from the following: Since the angle is a surface, and the line the boundary of the surface, it is clear that, in the same manner as the contingent angle is a divisible surface, so also its boundary, that is, the line, which bounds this surface angle, is divisible in its manner. Likewise the line which bounds the surface of the rectilinear angle is divisible in accordance with the divisibility of the surface. One can therefore cut off from the line, that bounds the surface of the rectilinear angle, the line which bounds the contingent angle, and therefore the line bounding the incidental angle is non-proportional to the line bounding the rectilinear angle by the one bounding the contingent angle. Since this line bounding the contingent angle is smaller than any rational fraction of a line which bounds a rectilinear or the incidental angle, the assertion is clear.
And therein you can observe, that there is a line before all divisibility of the line, which is incomprehensible by any divisibility, by which a straight line can cut a straight line in two. Even if this line is not divisible by a division, by which a line is divided by a line—in this respect it is like an unattainable endpoint—, nonetheless it is in its way divisible by a curve. Consequently that line is likewise called divisible, since it is the boundary of a surface, even if it may appear indivisible in comparison to a line bounded by a point. Just as the divisibility of a surface ends in a line, which is indivisible in respect to the surface, since it is not divisible in respect to surface, whereas seen as the surface's boundary line as such it is a divisible magnitude, just so the divisibility of the straight line by a straight line ends in a point, which is the boundary of the division and of the line, and as the boundary of the line is linearly indivisible, but seen for its own sake a divisible magnitude. It is thus possible, that a length is smaller or larger than another, but not by a specifiable rational fraction or a larger rational fraction, but rather by a smaller rational fraction. You can recognize therefrom, what one should think of the indivisible lines and points.
I therefore maintain: Even if one can draw a length from d toward eb that is proportional to the one sought, such that the divergence is not larger than an rational fraction, nonetheless no such length can be drawn, such that the divergence can be smaller than a rational fraction. Further I maintain: Even if innumerably many such lengths could be drawn, one would indeed be more precise than the other, but none the most precise of all.
Therefore, we want to see, which of all such lines the human mind can comprehend. It is clear: If a length, which must be proportional to the one sought, is extended by a definite part of its amount, for example, by one-third, one-fourth, or another fraction, then it always remains proportional. If therefore this length is extended, in the proportion of the segment lying between the endpoint on eb and the point e to the length ab, or in the proportion of the segment lying between the endpoint on eb and b to the length ab, it remains always proportional. The proportions are thus either of the kind that one does or does not arrive at the length sought by means of one of them. If not, then, by means of the length, which we set proportional to the unknown length sought, we can learn nothing of the length sought. Because, since the sought length is unknown and the extension does not lead us to it, but rather to a length which is larger or smaller than the unknown one, we shall not be able to find the divergence of the totally unknown one sought.
If you should maintain, that one comes to the sought length by the one extension and not by both, it will be the same one, because we do not know through which extension this should occur and where that line should lie, since indeed infinitely many lines can lie between e and b. If you should maintain, that the extensions be equal and nonetheless smaller or larger than the unknown one sought, once again one can never arrive at the one sought.
The proportional, of which the human mind can avail itself by this kind of procedure to arrive at the length sought, must necessarily be that one which presents, through both equal extensions, the one or the other as the length sought; and this is that line which is drawn from d towards the midpoint f between e and b. And it is the only one whereby the proportion of the distance from e to the length ab is the same one as the proportion of the distance from b to the length ab; extended in this proportion, that is, by one-fourth of its amount, it leads us to the length sought, as it is possible for us in this kind of procedure to reach the one sought, even if another length could be found more precisely in another manner.
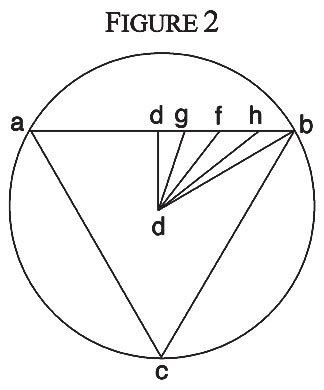 |
||
I have made clear to you everything that one can know about the equality of the perimeters of curvi- and rectilinearly bounded figures, namely, that the following comes closer to the truth: One cannot know equality, and even that which one can know most precisely in this area is made clear by a short proposition. With this I have fulfilled your wish, as well as I could. You must know: You have with that a method to investigate everything that can be known mathematically. In mathematical science, any proposition from which the precise equality of circle and square follows is impossible. And any proposition through whose opposite the precise equality could be introduced is necessarily correct. I even affirm: Whosoever understands in mathematical science, to lead every investigation back to this, has achieved the perfection of this art. Because here is absolutely nothing true from whose opposite the equality of circle and square would not follow. And that is the totally sufficient solution of any mathematical investigation.
But whatever one can know, in the transformation of figures and in numerically incomprehensible proportions, without ultimate precision however in the domain of every perceivable or specifiable error even of the smallest rational amount, I have made clear in the presentation. You know thereby, that the diameter is to the circumference as 21/2√1575 : 6√2700. True, that is not the precise value, but it is neither larger nor smaller by a minute or a specifiable fraction of a minute. And so one cannot know by how much it diverges from ultimate precision, since it is not reachable with a usual number. And therefore this error can also not be removed, since it is only comprehensible through a higher insight and by no means through a visible attempt. From that alone you can now know, that only in the domain inaccessible to our knowledge will a more precise value be reached. I have not found that this realization has been passed along until now.
Besides, it seems useful to observe that, as you see in this case, through a figure, for example, the square, one can not so precisely attain another, namely, the circle, or conversely, that it could not be given more precisely, even if the error does not step into view in any way. So in every investigation of the true, where we proceed from the one to a discernment of the other—from the known to the unknown—, the same is to be noted, namely, how one can arrive at the true in varied and multiple ways short of ultimate precision, by the one consideration more precisely than by the other, however by none perfectly precisely, even if the error does not step into view. The measure with which man strives for the inquiry of truth has no rational proportion to Truth itself, and consequently, the person who is contented this side of precision does not perceive the error. And therein do men differentiate themselves: These boast to have advanced to the complete precision, whose unattainability the wise recognize, so that those are the wiser, who know of their ignorance.
At the beginning I suggested to you, that you proceed upon this way of assimilation of the mathematical sciences to theology; because this is the more suitable way of ascension. Mathematical thinking has its seat in the true powers of the mind, since it regards figures in their true form, free of variable matter. From there one ascends more easily to the first form, that is, to the absolute Form of forms, through a kind of assimilation, after one has left the manifold of figures behind oneself. All theologians seek after a certain precision by means of which they can attain the eternity similar to the circle, the unique and most simple. But the infinite power is incommensurable to any non-infinite, just as the circle's area remains incommensurable to any area of a non-circle.
Thus, just as the circle is a figurative perfection, comprehending every possible perfection of figures in itself, and just as its surface embraces the surfaces of all figures and has nothing in common with any other figure, rather is in itself perfectly simple and unique, so is absolute eternity the Form of all forms, which in itself encloses the perfection, and so its omnipotence encompasses all power of the forms, of every kind, but without having a commonality with any other form. And just as the circular figure possesses, in the property of having neither beginning nor end, a certain similarity with eternity, and represents in its area, wherein it encloses the areas of all figures, a certain figure of omnipotence, and represents in the close connection with which it unites circumference and area, in a manner of speaking, a figure of the most loving and infinite connection, so we view in the divine essence the eternity, which in itself has omnipotence, and in both the infinite union. In eternity we view the beginning without beginning, and just this we name the paternal first cause. In the omnipotence, which comes from the beginning without beginning, we view the unbounded beginning from the beginning, in the infinite connection we view the most loving union of the beginning without beginning and of the beginning from the beginning. Namely in that we see eternity in the divine essence we view the Father. In that we see the power of eternity in the same essence, which cannot be other than infinite, since it is the power of eternity—of the beginning without beginning—, therein we view the equality of the eternal unity, that is, the Son of the Father. In that we see the most loving union of the eternal unity and its equality we view the Spirit of them both. In the simplest unity of eternity we thus see the strongest and most powerful equality, and conversely in equality, unity. Likewise, we also see unity and equality in the union. Without the unity of the eternal essence nothing can be. Without the equality of this unity nothing can be as it is. Without the infinite connection of being and simultaneously of so-being as it is, nothing can be. Therefore, without the triune Cause nothing can be.
All this is illustrated in the circle through its surface and the closest connection, through which the circle is most strongly connected to itself, cohering and by nature united. We observe accordingly: Just as all polygons, according to perimeter, according to area and the connection of both of these, are to the image of the circular figure, and just as every polygonal perimeter falls short of the circumference and every polygonal area remains disproportionately behind the area of the circle and likewise every connection of the two, just so are the different species of perceptible things to the Form of forms, so that the species of these perceptible things are in the comparison to God as the triangle, square, pentagon, etc., to the circle.
Each polygon has a definite perfection, outside of which it neither is nor can be. The being of the triangle cannot in any way exist outside of the essence of the triangle; it is the same with the square and so on. Thus every species rests, therefore, in its domain, which is enclosed by its limits. And outside it cannot, and does not wish, to be. Namely, the entire being would withdraw from the triangle, if it wanted to advance into the square, as is perfectly self-evident. Consequently, no species can be moved from its nature, through which it has being and so-being, to its annihilation, and therefore it rests in the limits of its specific nature. And this rest is its own, because, within the limits of its perfection, it holds the divine power in its own manner, and takes pleasure in it in loving union.
Each perceptible species is therefore in its manner a measure for the eternity, the power and the infinite union of love. Certainly in this measuring it has nothing proportional, since every polygon has a diminished power and surface, a weaker connection and union, and thus can have no rational proportion to the circular unity of eternity, to the inexhaustible content and to the infinite union, even if it has everything which it possesses in such a manner, that the power of the circle can participate in the nature of the triangle or square. The proportion of the perceptible species to the Form of forms is therefore that of the polygon to the circle. Further, since there are many modes of being of the triangle—one is the right triangle, another the acute, another the obtuse—, and in all such figures the various modes of being will sink down in variable matter—, all of these modes are also contracted individuals. Because the species, viewed in themselves and truly, appear in variable matter variously. The triangle can be produced closer to reality and more perfectly in gold than in water or another variable matter, and it is still more truly conceived in the mind than represented in any matter.
From this we therefore observe, that all polygons can be inscribed in a circle, and that in the circle all are more perfectly contained than in matter, since they are circle there; we see in this, that if all polygons can be inscribed in a visible circle, and the circle representing eternity is the actuality of every potential, then all species, according to actuality, are in the species or form of eternity themselves eternal Form, just as all polygons can be visibly inscribed in the circle. And just as the form of the triangle has in our mind a truer being than in variable matter, so have all species of things in the eternal Spirit or in the Word a truer being than in individual diversity; for there they are themselves eternal Truth.
Proceeding still farther, we observe the diversity of circles, and that only one can be the largest, the circle in perfected reality, the self-subsisting, eternal and infinite, to which one cannot ascend through ever so many circles, since, in things that admit of larger and smaller, one cannot come to the simply maximum. And in relation to this infinite circle we ponder wonderful and inexpressible things, which are treated more extensively elsewhere.
We thus maintain, there are entities of the species of the circle, which cannot be their own beginning, since they are not like the simply maximum circle, which alone is eternity itself; the other circles, which indeed do not seem to have beginning and end, since they are viewed through abstraction from the visible circle, are nonetheless, since they are not infinite eternity itself, circles whose being derives from the infinite first eternal circle. And these cirles in comparison to the polygons inscribed in them are, in a manner of speaking, eternity and perfect simplicity. They have a surface which exceeds the surfaces of all polygons non-proportionally, and they are the first image of the infinite first circle, even if they are not to be compared with it because of the infinity of the first. And there are entities that have a circular, interminable movement around the being of the infinite circle. They encompass within themselves the power of all other species, and from their encompassing power they develop all other species on the path of assimilation, and, beholding everything in themselves, and viewing themselves as the image of the infinite circle and through just this image—that is, themselves—, they elevate themselves to the eternal Truth or to the Original itself. These are the creatures bestowed with cognition, who embrace all with the power of their mind.
However, all figures attempt, as well as they can, to measure the power of comprehension of the eternal Truth. But just as the finite has no rational proportion to the infinite, so does God remain above every investigation the undiscerned precision itself, so that he remains not merely the unknown, but also the unknown precision itself, which cannot be discerned in any discernible object. Namely, every creature strives to define its God within the limits of its own essence; just as a triangle would like to triangulate the circle, a square to quadrate, and so on, with the other polygons, so also would the creatures bestowed with cognition like to discern God. But although God, who indeed has no parts, since He is infinite simplicity, exceeds none of all the different modes of measurement according to species by a specifiable part, He exceeds absolutely every measure of magnitude, because He is greater than any investigable measure. And in the same way He exceeds each of the fine measures for the smallest fraction, because He is the finest of all these fractions such that He can be precisely grasped neither through ascension nor descension.
But it is sufficient for every creature, if it attains God in its own species and in the manner possible for him. Namely, it is then in rest, since it neither seeks Him outside its species nor comprehends His Being. This sufficient comprehension, therefore, with which it attains Him according to the capacity of its nature, is the rest of the creature, since it is the satisfied movement of its nature.
This explains to us in an assimilating manner the investigation which we have conducted on the triangle, which we wanted to elevate to perimetric equality with the circle. And in the elevation of the triangle to equality with the circle we came to rest only in one manner, which we found to be the only precise one, even if deficient. This manner would not befit the peculiarity of the rectangle. If, however, the square would ascend to equality with the circle in its manner, then it could take pleasure in the rest attained, even though no absolute precision were to exist if only one other square were not more perfect in its species. The same holds for the rest of the polygons.
So every spirit comes to rest, if only it feels elevated in the admitted manner of its species to equality with the Infinite, even though the divine precision remains always unattained. This and infinitely many other things you can make clear to yourself. May it suffice to have thus treated the foregoing. Amen.
—translated by William F. Wertz, Jr.

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-771-8390
schiller@schillerinstitute.org
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2001- 2004 All Rights Reserved.
