
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Links
LaRouche | Music | Join | Books | Concerts | Highlights | Education | Health
Spanish Pages | Poetry | Dialogue of Cultures | Maps
What's New
An Introduction to
Pythagorean Sphaerics
(From An Introduction to Pythagorean Sphaerics—A Skit intendedto provide curiosity about why we study the heavens
by the Los Angeles LaRouche Youth Movement Sphaerics Group
from the Winter 2004 Fidelio)
Click here to read the script
Box 1
Astronomy of the Great Pyramid
Modern day “establishment” historians of science will fulminate against the notion of an advanced, ancient Egyptian astronomical tradition. Apparently counterposed to them, the “alternative” Egyptian history movement, created under the influence of the Synarchists, claims that ancient Egyptian astronomy derives from either space aliens, or psychotropic drugs, or secret societies. Plato, Herodotus, Diodorus Siculus, and the Great Pyramid itself tell a different story.
 |
||||
|
The Spinx, on the Giza plateau, site of the Great Pyramid
|
||||
 |
|||||
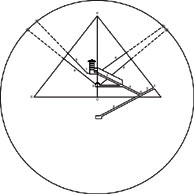
| The Great Pyramid of Khufu, (above), and a diagram of the Great Pyramid, showing observation shafts (below). |
|||||
 |
|||||
Sphaerics, or astronomy, dominated the architecture, religion, and economy of ancient Egypt, especially the magnificent Old Kingdom (2700-2180 B.C.E.), which built the Great Pyramid of Khufu as an astronomical observatory. Located on the Giza plateau, the Great Pyramid is stunning in the precision of its construction, a construction which could only have been meant for astronomical study. It is located precisely at 30° latitude, and is more accurately aligned to the four cardinal points than modern structures built to the same end. Within that alignment, the shafts built into the Pyramid, at crucial angles, allow for precise observations of key stars, such as Sirius, the North Star, and Orion's brightest star, as they transit the celestial meridian.
For the builders of the Great Pyramid to have accomplished such a task, the understanding of the regular motions of the stars and the celestial geometry of sphaerics had to have existed long before such an undertaking. The Pyramid Texts carved on the smaller pyramids of Saqqara, describe important astronomical cycles as myths in which, for example, figures such as Osiris and Isis are represented by the constellation Orion and the star Sirius, respectively. And, while carved in stone during the Old Kingdom, the origin of the Pyramid Texts is presumed to be much older.
—Susan Kokinda
Box II
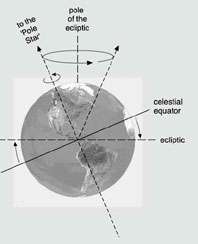
Precession of the Eqinoxes
 |
|||
| Left: Earth’s axis of rotation itself rotates around the “pole ofthe ecliptic.” | |||
 |
|||
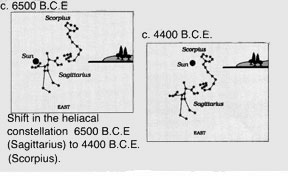
The 12 constellations of the Zodiac are the ones which follow the same path as the sun along the ecliptic, and Egyptian mythology and religion are filled with images of them. The dominance of a particular image, such as the scorpion, the bull, or the ram, often corresponds to the historical period in which that constellation was the heliacal constellation. For example, the death of Osiris, which Freemasons and Synarchists make a great mystical to-do over, can be seen simply as the disappearance of the constellation Orion from the sky, on the vernal equinox, which occurred around 6700 B.C.E.
—Susan Kokinda
Box III
The Legcy of Plato
A physical concept of magnitude was already fully developed by the circle associated with Plato, and expressed most explicitly in the Meno, Thaetetus, and Timaeus dialogues. Plato and his circle demonstrated this concept, pedagogically, through the paradoxes that arise when considering the uniqueness of the five regular solids, and the related problems of doubling a line, square, and cube. As Plato emphasized, each species of action generated a different species of magnitude. He denoted such species by the Greek word dunamis, the root of the English ‘dynamo’ translated as ‘power.’ The meaning of the term dunamis is akin to Leibniz’s use of the German word Kraft.
 |
|||
|
Plato (427-347 B.C.E)
|
|||
Plato's circle also emphasized, that this succession of magnitudes of higher powers, was generated by a succession of different types of action. Specifically, a simply-extended magnitude was produced from linear action, doubly-extended magnitudes from circular action, and triply-extended magnitudes from extended circular action, such as the rotational actions that produce a cone, cylinder, or torus. Plat's collaborator, Archytas, demonstrated that the magnitude with which a cube is doubled, is not generated by circular action, but by extended circular action, i.e., conic sections.
—Bruce Director
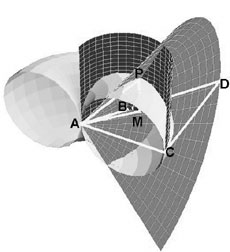 |
||
Archytas's Construction For
Doubling the Cube
Archytas developed a construction to find tow geometric means between two magnitudes. AC and AB. Magnitude AS is drawn as the diameter of circle ABC; AB is a chord of the circle. Using this circle as the base, generate a cylinder. The circle is then rotated 90 degrees about AC, Si it is perpendicular to the plane of circle ABC; it is then rotated about point A, to form a torus with nil diameter. (The intersection fo the torus and the cylinder produces a curve of double curvature.) Chord AB is extended until it intersects the perpendicular to AC at point D; this forms triangle ACD, which lies in plane of circle ABC, AB, and AC Triangle ACD is then rotated around AC, producing a cone. The cone, torus, and cylinder all intersect at point P. Perpendicular PM is then dropped from P along the surface of the cylinder, until it intersects circle ABC at point M; this forms right triangle AMP. Through this construction, a series of similar right triangles (only partially shown) is generated, which produces the continued proportion, AB:AM::AM:AP::AP:AC. Thus, AM and AP are shown to be the two geometric means between magnitudes AC and AB.
Box IV
The Platonic Solids
 |
||
 |
||
| Johannes Kepler discovered that the ordering of the visible planets correSponded to the ordering achieved by inscribing and circumscribing spheres around the five Platonic solids, in the order depicTed in this illustration from his “Mysterium Cosmographicum.” |
||
The proof that no other regular solids but these—the pyramid, cube, octahedron, dodecahedron, and icosahedron—can be constructed in visible space, was tantamount to the assertion that, contrary to textbook Euclideanism or the dead world of Isaac Newton, physical space was not “empty,” but instead shaped by unseen boundary conditions inherent in the possibilities of physical action. What appear to be the axioms, definitions, and postulates of mathematics, must yield to the causal relations of physics; in fact, the very proof of the uniqueness of the Platonic solids—one of the greatest achievements of Greek geometry, which required the development of a theory of proportions able to deal with incommensurable species of magnitudes (powers)—represented, paradoxically, a complete overturning of the method of deductive (logical) proof upon which it was based.
Although Plato presents these issues directly in his Timaeus, they are also embedded at the heart of the Republic, in the twinned metaphors of The Cave and the Divided Line. Here, we see that what we know truly, we know metaphorically—but only by reference to an unseen Power which animates and unifies the more immediate aspects of our experience.—Ken Kronberg
Box V
Mathematical Models vs. Truth
 |
||||
|
Johannes Kepler
|
||||
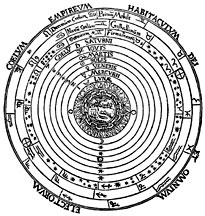
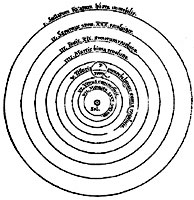
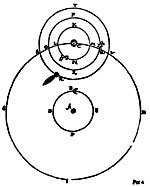
(a) The Ptolemaic system, with the Earth at the center and all the planets and the sun moving around it in perfect circles. (b) The Copernican system, with the sun at the center, and all the planets, including the Earth, moving around it in perfect circles. (c) The system of Tycho Brahe, in which the Earth is at the center, and all the planets move about the sun in perfect circles, while the sun moves about the Earth in a perfect circle.
—Bruce Director
 |
||||||||||
 |
||||||||||
 |
||||||||||
|
(a) Ptolemaic system:
Earth-centered. |
(b) Copernican system:
sun-centered. |
(c)System of Tyco Brahe:
mixed Earth and sun-centered. |
||||||||
Box VI
Kepler’s Physics of Non-Constant Change
 |
|||
 |
|||
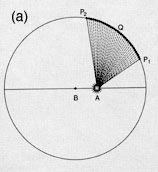
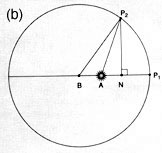
(b) Kepler measured these areas. The area swept out as the planet moves from P1 to P2 is the white area (P1-P2-A). That area is measure by the portion of the circle, P1-B-P2. minus the triangle P2-B-A. The area of that triangle is the distance BA times the height P2-N. But, the line P2-N, as Nicolaus of Cusa showed, is incommensurable with the arc P1-P2. Thus, the principle of non-uniform planetary motion is dependent on magnitudes which are not susceptible of precise calculation. This gave rise to the famous “Kepler problem”: If Kepler knew where the planet had been, he could calculate what portion of the orbit (time) had elapsed. But, owing to the transcendental relationship between the line and curve, he could not precisely calculate where the planet would be when an equal amount of time would have elapsed. Kepler called on future geometers to solve this problem, which provoked Leibniz to develop the calculus.
 |
|||
 |
|||
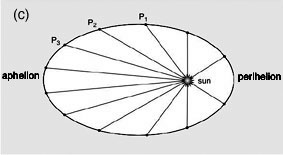
(c) Keplers’s initial discovery of the “equal areas, equal times” principle was developed under the assumption that the orbit was circular, with the sun at an eccentric point. After comparing his results to the true observations, Kepler found he was 8′ of arc off. It is a tribute to Kepler’s genius, that he saw that this small discrepancy was a matter of principle, not simply a minor error. He subsequently revised all his work, and discovered that the planetary orbits were ellipses with the sun at one focus.
(d) Kepler’s diagram from the New Astronomy. The dotted curve is an ellipse. As you can see, this ellipse is very close to a circle, but as Cusa has forecast in On Learned Ignorance, there is no perfectly circular motion in the created world.
—Bruce Director.
Box VII
‘Follow the Drinking Gourd’
“When the sun comes back
And the first quail calls,
Follow the Drinking Gourd.
For the old man is a-waiting for to carry you to freedom,
If you follow the Drinking Gourd. ...”
 |
||
 |
||
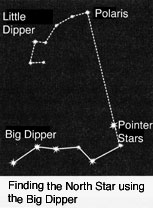
The idea of using the vast, unfettered expanse of the starry heavens to find one's way to freedom, became more than just a navigational “trick,” but a metaphor for the quest for freedom. Frederick Douglass, the great leader of the movement to free the slaves, named his newspaper The North Star. He understood profoundly that science means the liberation of man; only if your oppressors can keep you ignorant, can they control you.
As most people know, the slaves were helped along their way by the “Underground Railroad” of people who would feed and safehouse them, and direct them on to the next “station.” The most famous “conductor” on the “railroad” was Harriet Tubman, known as the Moses of her people. Frederick Douglass wrote to her in 1868: “I have had the applause of the crowd and the satisfaction that comes of being approved by the multitude, while the most you have done has been witnessed by a few trembling, scared, and foot-sore bondsmen and women, whom you have led out of the house of bondage, and whose heartfelt 'God bless you' has been your only reward. The midnight sky and the silent stars have been the witnesses of your devotion to freedom and your heroism.”
 |
|||
|
Helping slaves to freedom on the “Underground Railroad.”
|
|||
Tubman, herself a slave in Maryland, had escaped to freedom at the age of 28, with only the North Star as her guide. She then helped more than 300 others to do the same, telling them: “Children, if you are tired, keep going; if you are scared, keep going; if you are hungry; keep going; if you want to taste freedom, keep going.” She kept a six-shooter under her skirt, to provide a little encouragement to anyone who fearfully complained that he could not take another step. Tubman summed up her life's work: “On my Underground Railroad I nebber run my train off de track and I nebber los' a passenger”—a quote which was inscribed on a plaque in her honor by the citizens of Auburn, New York, at the court house in Cayuga County, where she died in 1913.
—Susan Welsh
What is the Schiller Institute?
Lyndon and Helga LaRouche Dialogues, 2005
Lyndon and Helga LaRouche Dialogues, 2004
Eurasian Landbridge and Economy
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine
Writings of Other Great Thinkers
Biography of Friedrich Schiller
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Links
LaRouche | Music | Join | Books | Concerts | Highlights | Education | Health
Spanish Pages | Poetry | Dialogue of Cultures | Maps
What's New
© Copyright Schiller Institute, Inc. 2005. All Rights Reserved.