Schiller Institute Gauss Fundamental Theorem -Diagrams by Bruce Director

SCHILLER INSTITUTE

Figure 1: A succession of algebraic powers is generated by a self-similar spiral. For equal angles of rotation, the lengths of the corresponding radii are increased to the next power.

Back to Article

Figure 2: Leibniz' construction of the algebraic powers from the hanging chain
Back to Article

Figure 3: An example of the three solutions to the trisection of an angle
Back to Article

Figure 4: The unit of action in Gauss' complex domain.
Back to Article

Figure 5: In (a) the lengths of the radii are squared as the angle of rotation doubles.
Back to Article

In (b) the lengths of the radii are cubed as the angle of rotation triples.
Back to Article

Figure 6: Squaring a complex number.
Back to Article

Figure 7: Cubing a complex number.
Back to Article

Figure 8: The sin of x is zP and the cosine of x is 0P. The sine of 2x is QP' and the cosine is OP'.
Back to Article

Figure 9: Variations of the sine and cosine from the squaring of a complex number.
Back to Article

Figure 10: Gaussian surface for the second power.
Back to Article

Figure 11: Gaussian surface for the third power.
Back to Article

Figure 12: Gaussian surface for the fourth power.
Back to Article

Figure 13: Combined Gaussian surfaces for algebraic equations. (a) combines the surfaces based on the variations of the sine and cosine for the second power.

Back to Article

(b) combines the surfaces based on the variations of the sine and cosine for the third power.

Back to Article

Figure 14: Roots of algebraic equations represented in a Gaussian surface. (a) is the intersection of the surfaces in 13(a) with the flat plane.

Back to Article

(b) is the intersection of the surfaces in 13(b) with the flat plane.

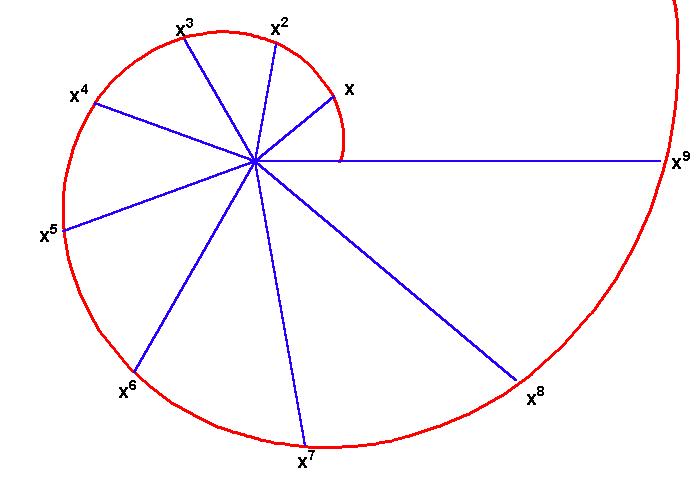
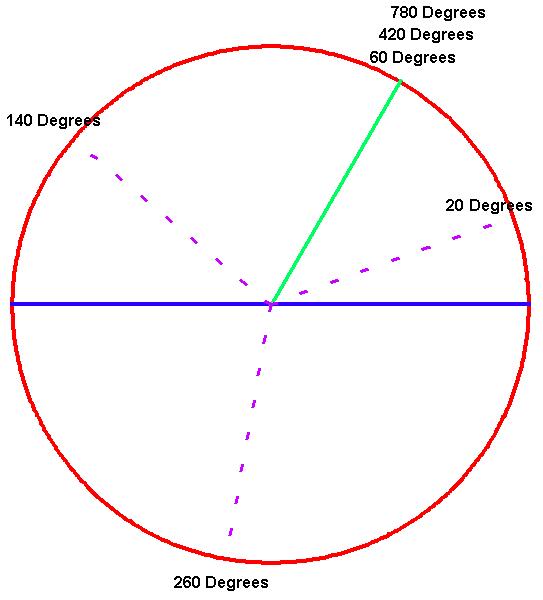
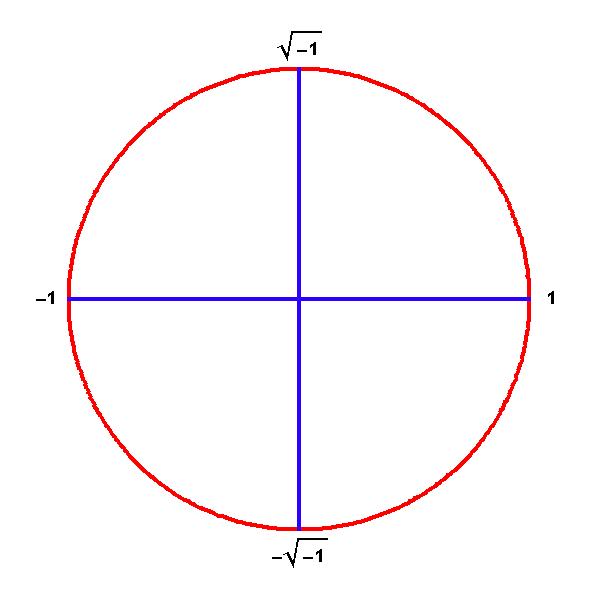
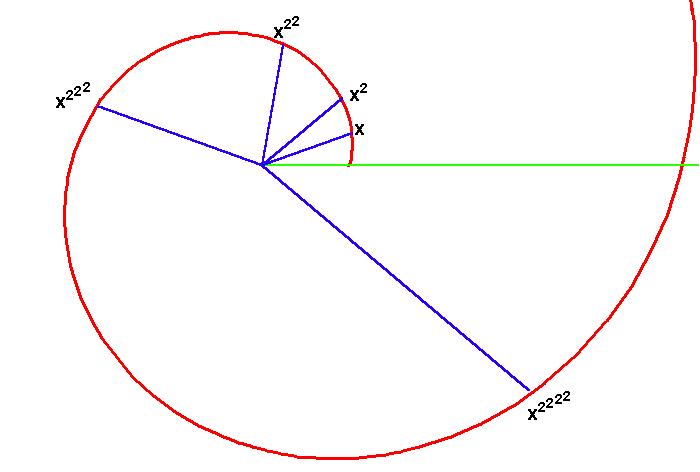
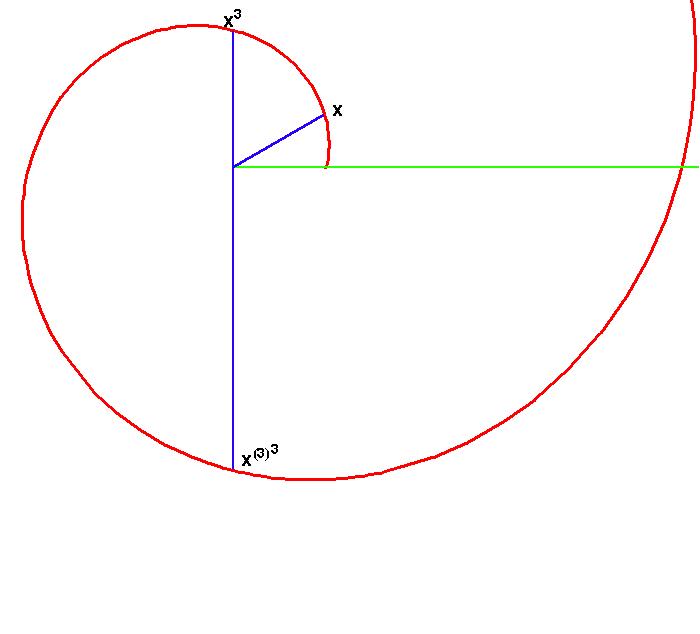
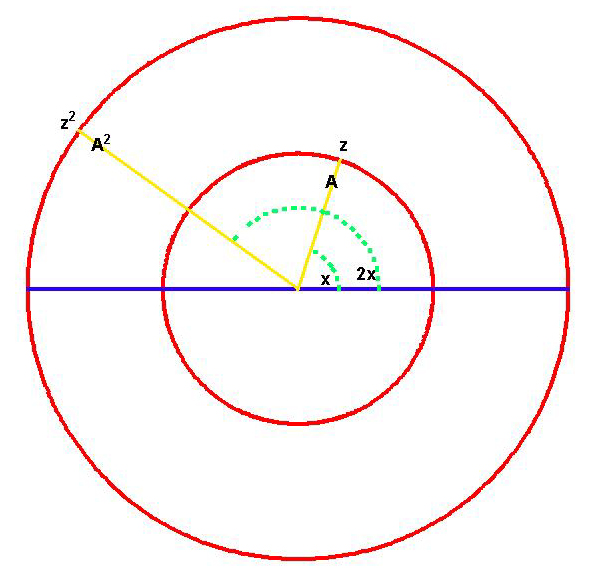
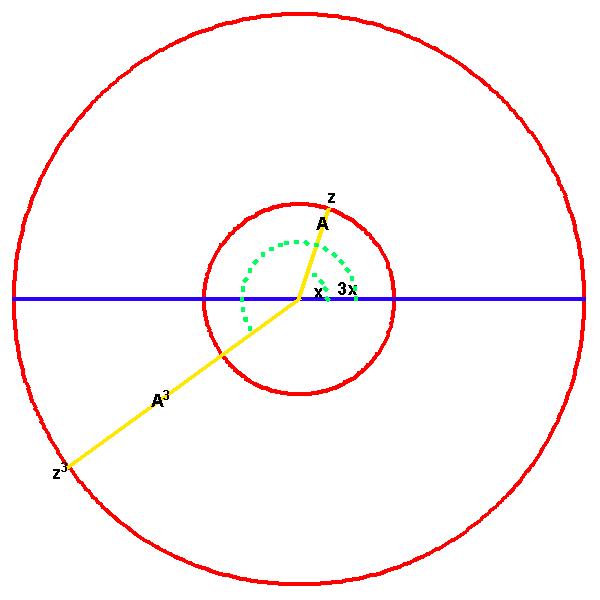
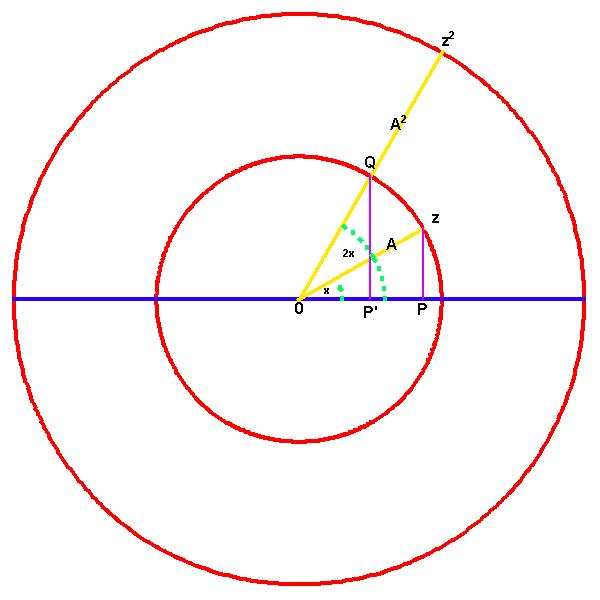
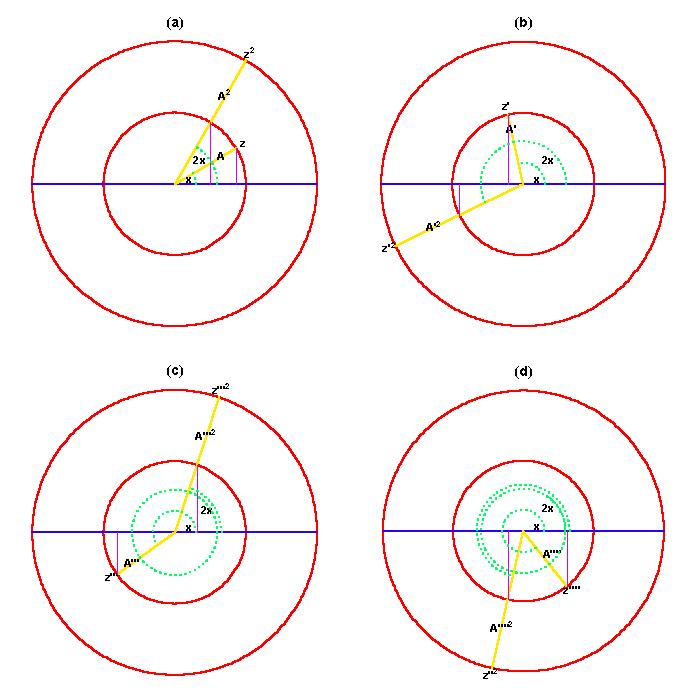
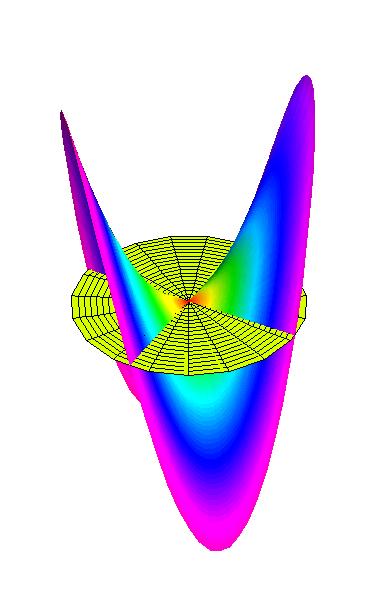
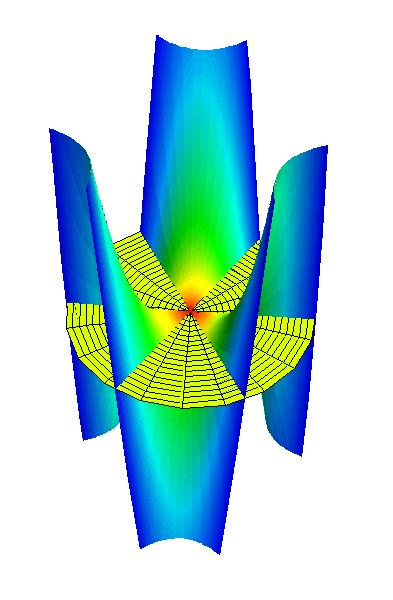
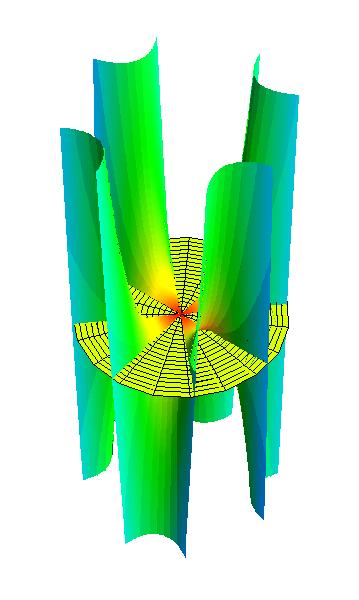
Back to Article

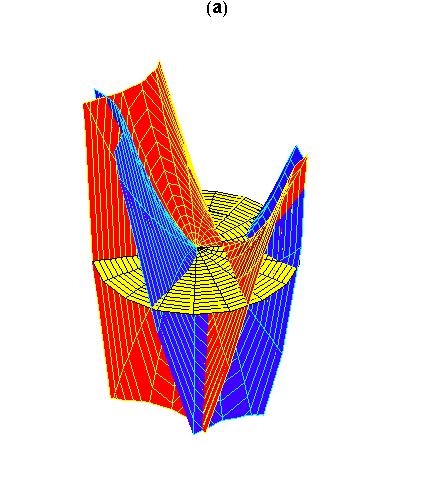
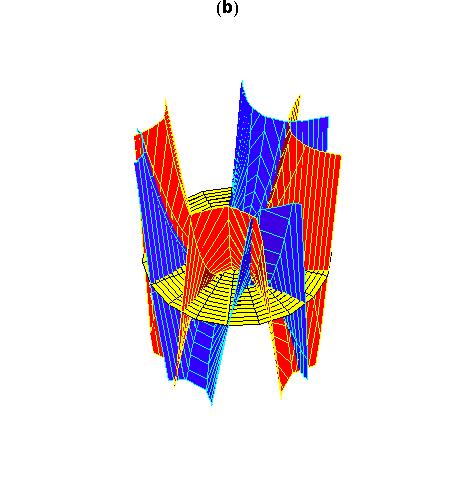
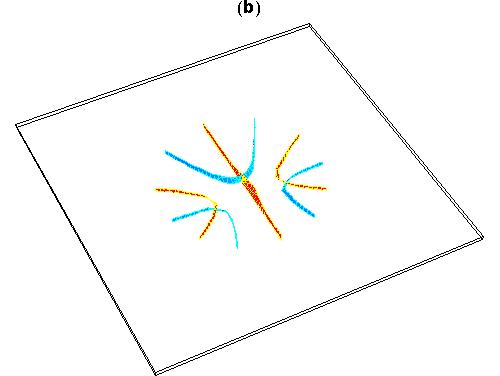
schiller@schillerinstitute.org

The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368

Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.

Contributions and memberships are not tax-deductible.

VISIT THESE OTHER PAGES: